Формулы и доказательства: понимая «как» и «почему»
Чтобы совершить прорыв, человечеству всегда приходилось отказываться от привычного понимания мира.
Один из первых таких кризисов произошел в античной математике. Греческим геометрам пришлось смириться с существованием иррациональных чисел — величин вроде корня из двух. Их нельзя точно выразить никакой дробью с целыми числителем и знаменателем. Проблема рождалась из геометрической практики: диагональ квадрата можно было начертить и измерить, но при этом оказывалось, что ее длина в привычном смысле несоизмерима со сторонами квадрата, частью которого она является. Это не укладывалось в парадигму мышления, построенного на пропорциях и отношениях.
Примерно в ту же эпоху математика столкнулась с еще одной умопомрачительной идеей — нулем. Для расчетов потребовалось ввести мысленный эквивалент «ничего», при этом обозначив его чем-то и включив в систему чисел. Философов это приводило в замешательство: как можно мыслить небытие как объект, о котором можно рассуждать и с которым можно производить операции?
С развитием человеческой мысли этот процесс ухода от интуитивности только ускорялся. Например, для расчетов во время торговли, пришлось принять отрицательные числа — величины, которые меньше нуля и которые невозможно напрямую интерпретировать как длину или количество предметов. Затем появились комплексные числа, долгое время воспринимавшиеся как чистая уступка формализму. Однако со временем выяснилось, что именно они оказываются незаменимым инструментом для описания вполне реальных процессов. Кстати, сегодня комплексные числа лежат в основе расчетов электрических цепей с переменным током.
Несмотря на возрастающий уровень абстракции, классическая естественная наука всегда строилась как цепочка наблюдений и логических умозаключений. Мы наблюдали явление, например падение тел в поле силы тяжести, затем искали устойчивую закономерность, многократно измеряя и сопоставляя, и наконец создавали математическую модель.
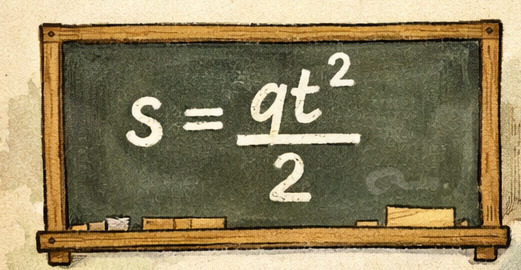
Такие модели могут не только в некотором смысле предсказывать будущее, но и раскрывать внутреннюю природу наблюдаемых закономерностей. Например, мы видим, что в формуле, описывающей свободное падение, отсутствует масса падающего тела. Значит, все тела падают одинаково, если, конечно, пренебречь сопротивлением воздуха.
Другая модель, которая описывает колебания маятника, одновременно открывает нам понятие резонанса и указывает, на какой частоте он возникает. Если сказать проще: у колебательных систем есть «любимая» частота, на которой они особенно сильно раскачиваются. Если толкать маятник случайно, он будет привычным образом колебаться, но если подталкивать его с нужным ритмом, каждый новый толчок будет добавлять энергии ровно в нужный момент и сила колебаний начнет резко расти. Математическая модель превращает этот феномен в объяснимое логическое следствие уравнений динамики и делает предсказуемым: теперь мы понимаем не только то, что резонанс существует, но при каких условиях он происходит. В некотором смысле математическая модель и ее решение работают как «ключи» от «замка» изучаемого явления или объекта.
Несмотря на мощь математического инструментария, в мире всегда существовали задачи, которые сопротивлялись этому «открыванию» особенно сильно. Динамика двухзвенного маятника — это классический пример подобной задачи. Математический аппарат, известный науке на момент написания этой статьи, не может решить уравнения, описывающие движение этой системы. Возможно, нужных инструментов просто еще не изобретено. Возможно, в принципе нет формулы, которая описала бы поведение двухзвенного маятника.
Так или иначе, «ключа» от этого «замка» у нас пока нет. Именно такие «нерешаемые» задачи исторически двигали науку вперед. Чтобы решать практические проблемы, математики изобретали новые методы, а физики — новые модели: от механики Лагранжа, которая переопределяет классическое школьные ньютоновское описание «F = ma» через энергии и вариационные принципы, до целых ветвей анализа и теории уравнений. Но даже лучшие умы, как и все люди, всегда хотели подсмотреть в конец «учебника», чтобы узнать правильный ответ, если решение не давалось…
Численные методы: «как» без «почему»
Почти с самого начала формализации естественных наук, появились методы, которые в некотором смысле обходили ограничение классического познания. Они позволяли получать очень близкий к точному ответ, но не выводили общей закономерности в виде формулы или теории. К таким методам относятся, например, метод Ньютона для решения уравнений и другие численные схемы. Формально они не объясняют, почему некоторый объект ведет себя так или иначе, а лишь могут шаг за шагом приблизиться к описанию его поведения в одном конкретном случае. Говоря совсем грубо, «подогнать» ответ под уравнение модели перебором. При этом не всегда ясно, насколько результат надежен: маленькие ошибки округления могут накапливаться, а в сложных системах приводить к результатам, не соответствующим действительности.
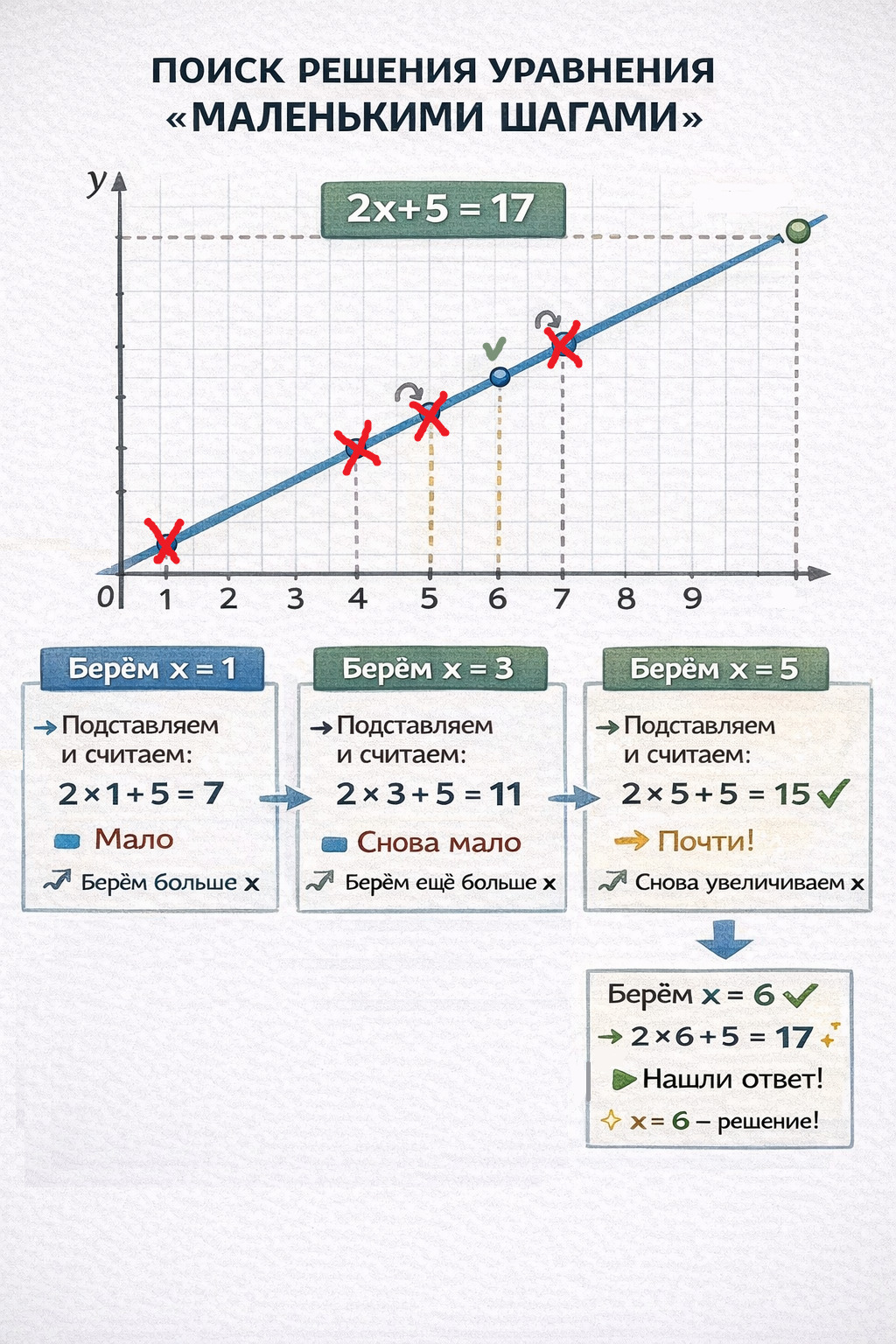
Появление компьютеров значительно повысило эффективность применения численных методов и привело к прорыву в прикладной науке и инженерии. Скорость, с которой машины выполняют вычисления, на много порядков превосходит человеческую, а сами численные методы, по удачному совпадению, хорошо поддаются алгоритмизации. Типичная схема проста: решить уравнение модели приближенно на одном шаге, подставить результат в следующий и повторить эту процедуру много раз.
Так людям удалось научиться работать с процессами и системами, которые прежде были недоступны для анализа. Однако вместе с этим возникла принципиально новая эпистемологическая проблема. Теперь, чтобы получить результат, нам не всегда нужно находить «ключ» от «замка». Во многих случаях задачу можно взять силой, подобрав ответы пригодные для практического использования при помощи численных алгоритмов. Мы получаем ответ, знаем, что он правильный, но в действительности не понимаем, откуда он взялся.
Хороший пример — уравнения Навье-Стокса, которые описывают движение сплошных сред: воды, воздуха, газа. Это полезно для расчетов в прикладных задачах, связанных с аэродинамикой. В общем виде решение этих уравнений неизвестно. Тем не менее на практике с ними успешно работают. Непрерывное численное пространство разбивают мелкой сеткой и с помощью компьютера шаг за шагом рассчитывают, как меняются скорость, давление и другие величины во времени. В итоге получается не привычное решение в виде формулы, а лишь приближенная с хорошей точностью картина потока для конкретного частного случая. Феномен возникновения турбулентности, знакомой всем летавшим на самолете, в этом смысле особенно показателен. Мы наблюдаем ее, моделируем конкретные случаи, умеем учитывать ее последствия в расчетах, но не располагаем знанием, объясняющим турбулентность в общем виде.
Похожая ситуация возникает и с двойным маятником. Уравнения его движения известны, но общего решения пока нет. Численные методы снова позволяют заглянуть внутрь системы, построить траектории, на первый взгляд почти хаотического движения, исследовать его свойства. Мы видим поражающие своей красотой и сложностью зависимости, можем использовать их на практике, но при этом не имеем компактного теоретического описания, которое порождало бы все это разнообразие. Нам снова доступны только следствия, но не предпосылки и фундаментальные законы.
Нечеткие подходы и искусственный интеллект: ответы без «как» и «почему»
Параллельно с численными алгоритмами, отчасти используя их инструментарий, развивались другие подходы для взлома «замков» закономерностей — статистические и вероятностные методы работы с неопределенностями и плохо формализуемыми системами. Эти инструменты позволили описывать закономерности, которые проявляются на уровне больших массивов наблюдений, но ускользают от точного детерминированного описания. Такие методы оказались особенно востребованы в биологии и экономике — областях, где эксперимент трудно изолировать, а большая вариативность является неотъемлемым свойством изучаемых процессов. Со временем из этих подходов выросло машинное обучение. Накопление больших объемов данных дало возможность строить обобщенные модели, которые не выводятся из принципов мироустройства, а сами подстраиваются под наблюдения. В основе такого подхода лежит допущение, что искомая закономерность существует и достаточно устойчива, а значит, похожие входные условия приводят к похожему поведению системы. Чаще всего это предположение оправдывается. Модели работают и дают полезные практические результаты.
Однако здесь происходит еще один значимый сдвиг в структуре нашего незнания. Теперь мы не только «подгонкой» ищем частные решения для разработанных нами общих моделей. Теперь мы используем универсальные модели для частных случаев и решаем их универсальными численными методами. Любая задача стала решаться по схеме: собрать много данных — обучить модель — получить результат. Так мы можем эффективно работать с объектами вроде изображений или естественного языка без их математической модели.
Теперь мы больше не понимаем не только почему система ведет себя так или иначе, как это было при использовании численных решений без аналитической формулы, но и на базе какой закономерности строится решение. Мы снова получаем рабочий инструмент, но цена этого — еще больший разрыв между нашими возможностями и нашим знанием.
Мы перестали понимать мир?
В научной традиции давно существует точка зрения, согласно которой случайность не является свойством мира как такового, а отражает лишь ограниченность нашего знания. Классический пример — бросок монетки. В принципе его исход можно было бы предсказать, если бы мы точно знали форму монеты, начальное положение, силу и направление броска, сопротивление воздуха и все микроскопические возмущения среды. Все же объекты вроде подброшенной монеты, двойного маятника или турбулентного потока воздуха обладают высокой чувствительностью к начальным условиям: ничтожная погрешность на старте со временем приводит к радикально разным исходам. Формально такие системы могут быть полностью детерминированными, но практически — непредсказуемыми. Для человеческого масштаба измерений и вычислений эта непредсказуемость неустранима, и именно она заставляет нас говорить о случайности.
Но даже если оставить в стороне фундаментальные физические вопросы, на уровне человеческого опыта и сознания реальная случайность может играть самостоятельную роль. Если в мире действительно есть место свободе воли или хотя бы поведению, которое принципиально не сводится к точному предсказанию, то работа с неопределенностью перестает быть временной уступкой и становится необходимой частью научного инструментария.
Если посмотреть на ситуацию под этим углом, становится ясно, что методы, работающие со случайностью и неопределенностью не признак кризиса и не отказ от научной строгости. Это ответ на расширение круга задач, с которыми мы сталкиваемся. Численные, вероятностные и нечеткие подходы — это не инструмент «взлома» и не замена теории, а скорее новый «ключ», который открывает дверь, за которой нет простых формул и однозначных предсказаний, но есть сложные, нестабильные и трудно описываемые закономерности, с которыми, тем не менее, можно осмысленно работать.


