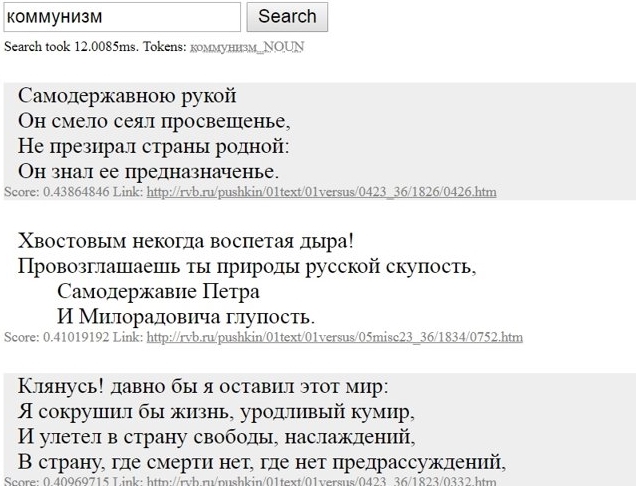
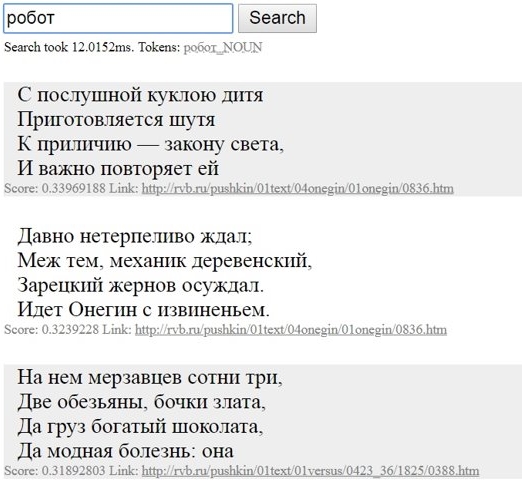
Как найти «то, не знаю что», а если точнее — совершить нечеткий поиск? Вот бы можно было найти в интернете «похожую мысль», «что-нибудь по теме» или «такое же по смыслу». Жаль, что напрямую со смыслом слов Гугл пока что работать не умеет… Зато нечто похожее умеет маленький поисковик по стихам Пушкина — посмотрите:
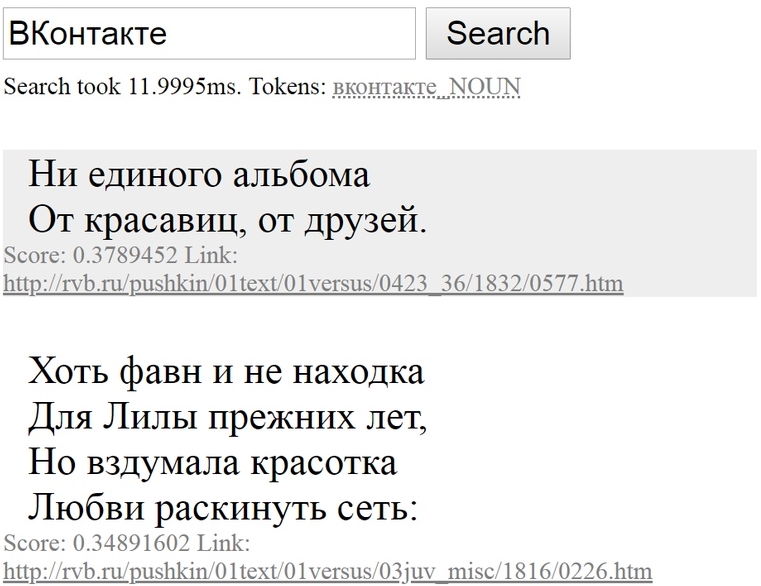
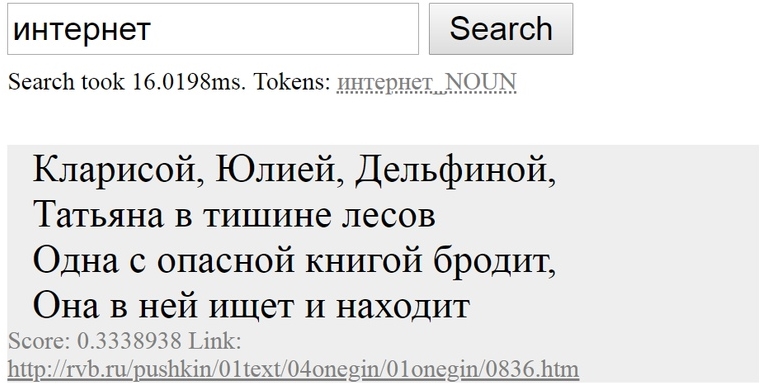
Как так получилось, что, хотя Пушкин не писал про интернет, поисковик нашел в его стихах строчки про книгу, в которой можно «искать и найти»? Ответ: благодаря семантическим векторам. Давайте разберемся.
Как это работает?
Давайте спросим себя, как узнать значение незнакомого слова, если под рукой нет словаря? Допустим для сложности, что перед нами инопланетный язык, где слова состоят из букв, но одно из слов для нас ни на что не похоже и ничего не напоминает. Может, какая-то часть смысла «спрятана» в приставке или суффиксе — как, например, мы могли бы предположить, если бы сравнили слова «уходить» и «подходить», или «стол» и «столик»?
Интересную мысль на этот счет в 1957 году выразил английский лингвист Джон Руперт Фёрс, сказав: «Слово узнаешь по его окружению». А значит, можно догадаться, что «вилка» скорее связана со столовой, нежели с зоопарком, если она чаще встречается в текстах рядом со словами «блюдо» и «завтрак», чем со словами «зебра» и «шимпанзе». Грубо говоря, на этой гипотезе строится основа дистрибутивной семантики — направления лингвистики, которое вычисляет, насколько близки два слова по смыслу, исходя из частоты их совместной встречаемости в текстовых корпусах. Так можно найти синонимы и антонимы к слову или классифицировать его в тематический «отдел», автоматически определить тематику документа, не давая прочесть его человеку, постараться смоделировать перифразы или выяснить правила сочетаемости слов.
Для таких операций каждому новому слову придется присвоить набор чисел, характеризующий его смысл. Этот набор называется семантическим вектором слова. Откуда его взять? Конечно, потребуется корпус текстов, то есть их большая и разнообразная коллекция. В коллекции нужно найти все уникальные слова и подсчитать, сколько раз каждое слово встретилось в корпусе, чтобы исключить из выборки самые частые и самые редкие (они внесут слишком большую статистическую погрешность, если их учитывать). А теперь — вообразим большую таблицу размером n * n, где n — это число уникальных слов в тексте. (Сегодня такой таблицей не пользуются, но она хороша для наглядности). Каждая строка и столбец в ней — это какое-то слово, к примеру, вот так:
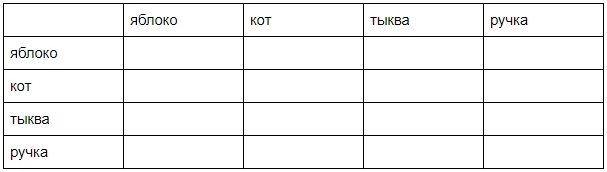
Насколько большой будет такая таблица? Конечно, это зависит от числа уникальных слов в тексте. Если корпус достаточно большой, то и таблица будет просто огромной, а это неудобно для вычислений. Но о вычислениях чуть позже.
А пока — заполним таблицу. В ячейках будем писать число раз, которое слово из столбца и слово из строки встретились в тексте «рядом», то есть на расстоянии не более n слов. Это расстояние лингвисты называют «шириной окна» поиска: по опыту можно судить, что неплохие результаты получаются, если брать ширину равной, например, 10. Подсчитывать будем не вручную: на компьютере наши действия выглядят как дробление текста на отрывки из подряд идущих N слов (их называют N-граммы) и подсчет количества N-грамм, в пределах которых встретились два слова.
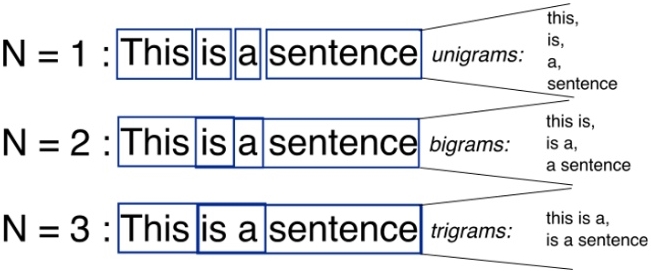
На картинке — пример разбивки предложения на N-граммы с шириной окна в 1, 2 и 3 слова. Обратите внимание на то, что N-граммы идут «внахлёст».
После такого подсчета для текста получаем статистику того, сколько раз каждое слово встречается на расстоянии N от каждого другого слова: то есть набор чисел, который можно представить в виде длинной цепочки (иначе говоря, многомерного вектора). Но — важный момент! — поскольку многие слова в больших текстах, как показывает практика, вообще не встречаются рядом друг с другом, многие числа в этом векторе будут нулевыми, а размерность — просто огромной. Значит, целесообразно сократить его размерность без существенной потери смысла, для чего существует множество хитрых математических методов: например, случайное индексирование и сингулярное разложение. Фокус в том, что нужно «выбросить» из вектора ненужные числа так, чтобы его сходство с векторами близких по смыслу слов осталось велико, а с дальними — минимально.
В 2013 году Томаш Миколов, ученый из Чехии, разработал систему Word2vec, которая не строит никаких огромных таблиц и векторов на тысячи элементов, чтобы потом сокращать их. Она сразу строит векторы заданной «короткой» размерности. Метод Миколова состоит в применении двух нейронных моделей: continuous bag-of-words (CBOW) и skip-gram. Первый предсказывает слово на основе данного контекста, а второй — наоборот, старается угадать контекст данного слова. В результате слова, встречающиеся в тексте в одинаковом окружении (а следовательно, имеющие схожий смысл), в векторном представлении будут иметь близкие координаты.
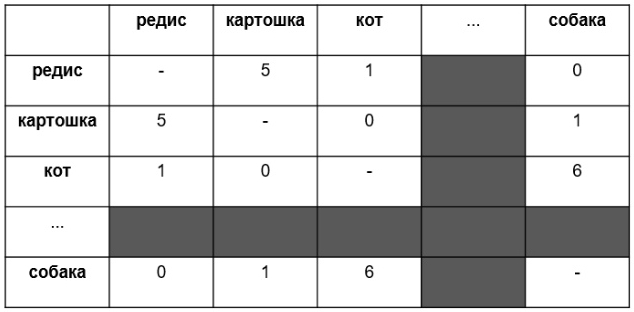
Что теперь можно делать с семантическим вектором? Можно, к примеру, рассчитать их косинусную близость, удобный математический показатель схожести векторов. Чтобы получить этот показатель, математики делят скалярное произведение векторов на произведение их модулей. Кроме того, с многомерными векторами можно проводить те же операции, что мы делали в школе с двухмерными — можно складывать их, вычитать, и даже строить пропорции. Именно на этих принципах, кстати, работает «семантический калькулятор» на сайте RusVectores. Посмотрите, если еще не видели.
Кроме калькулятора на RusVectores есть еще одна интересная вещь: готовые наборы семантических векторов для огромного числа слов, полученные после обработки различных корпусов текстов алгоритмами word2vec с разными параметрами. Эти наборы (они называются «векторные модели») можно скачать и использовать как готовую базу данных семантических векторов. Пользуясь этой возможностью, пользователь GitLab opennota написал семантический поисковик по стихам Александра Сергеевича Пушкина.
Интерфейс программы — это поле запроса, где пользователь может ввести слово или группу слов. Введенный запрос сохраняется в буфер обмена, где морфологический анализатор pymorphy2 распознает формы и леммы слов.
Для каждого слова запроса из предварительно рассчитанной модели word2vec извлекается семантический вектор. Программа может использовать любую из векторных моделей, представленных на сайте проекта RusVectores. В случае, если поисковой запрос содержал несколько слов, их векторы суммируются и нормализуются. Под нормализацией здесь мы понимаем деление каждого элемента вектора на его длину, то есть на сумму квадратов всех элементов. Это позволяет получить вектор того же «направления», если так можно сказать о векторе, у которого 300 координат, но унифицированная «длина». Такой вектор (его называют еще «единичным») хорошо подходит для вычислений.
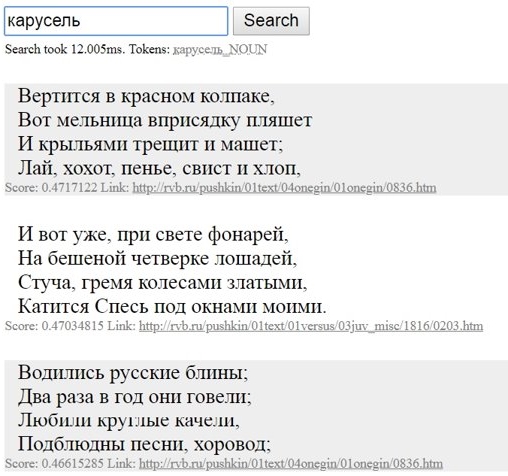
Извлечение векторов отдельных слов, их суммирование и нормализация происходит также для каждого четверостишия из используемой базы данных: эта процедура реализуется при запуске программы. В результате для каждого четверостишия составляется единый семантический вектор. (Эта операция проводится только один раз, при запуске программы, а потому мы поставили её на второе место для удобства иллюстрации). После получения нормализованного вектора поискового запроса рассчитываются показатели косинусной близости вектора запроса и каждого из векторов четверостиший. Показатели сравниваются и программа выдает строфы, чей семантический вектор ближе всего к вектору слов из поискового запроса.
Поиск дает результаты и тогда, когда, очевидно, слова из поискового запроса не могут встречаться в произведениях Пушкина (например, «звездолет»).
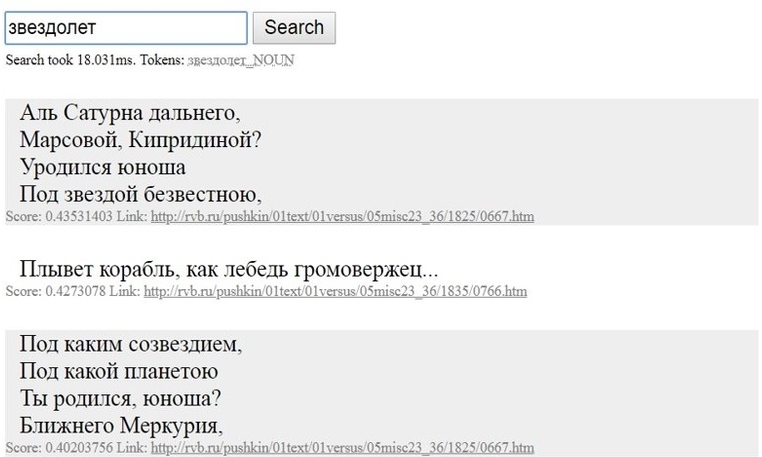
Некоторые слова из первой, самой » похожей» строфы («Сатурн, Марс, звезда») явно указывают на «космическую тематику», хотя сами слова «космос» или «звездолёт» в четверостишии отсутствуют. А второй так и вовсе говорит скорее о мореходстве, но слово «корабль» явно встречалось в корпусе текстов и в значении «космический корабль», то есть «звездолет». Данный пример демонстрирует, что при помощи инструментов word2vec и проекта RusVectores можно проводить семантический анализ и категоризацию текстов, выполняя поиск по нечетким критериям. Исследователь, работающий с подобной системой, сможет отыскать нестандартные контексты и значения лексических единиц на большом объеме данных.
А на сладкое — посмотрите на некоторые примеры поисковых выдач программы, когда ее попросили найти слова, которых никак не могло встретиться у Пушкина: