У вас когда-нибудь было такое, что срочно надо разобраться в новой области, но про нее неизвестно вообще ничего, непонятно даже, что писать в поисковом запросе?
В такие моменты пригодился бы поисковик, куда можно загрузить документ или сайт на нужную тему и подождать, пока машина сама не определит, что за темы затрагиваются в запросе и в каких пропорциях. Установив темы, поисковик найдет похожие документы или сайты, покажет, что в теме сейчас актуально, что устарело, какие темы смежные и с чего начать знакомство с ними — значит, не придется искать всё это вручную.
Такой поисковик должен уметь определять темы, о которых идет речь в документе. Кстати, документом может быть сайт, учебник или служебная записка — это неважно. Вручную темы не опишешь — их слишком много, плюс часто непонятно, что делать, если какая-то тема появилась на стыке других, расширилась, потеряла актуальность? Поэтому, чтобы не страдать самим, программисты нашли способы находить в текстах и описывать темы автоматически. Этот процесс называется тематическим моделированием, и о нем мы сегодня расскажем.
Идея тематического моделирования:
- Тема — это просто список слов.
- Чем чаще слова из этого списка встречаются в документе, тем сильнее он связан с темой
К этой идее прилагается еще пара моментов. Алгоритмы тематического моделирования работают не с одним большим текстом, а с коллекцией отдельных документов, потому что важно научиться разбивать по темам именно целые тексты, а не предложения или абзацы. В обучающую выборку документов, неважно, собрана она машиной или человеком, входят тексты на разные темы, максимально непохожие друг на друга, то есть состоящие из разных слов.
Вторая особенность — одно и то же слово может относиться к нескольким темам сразу, а документы являются смесью нескольких тем. Поэтому тематическое моделирование описывают как алгоритмы «мягкой кластеризации»: такие алгоритмы разрешают одной и той же сущности принадлежать сразу к нескольким классам.
Охарактеризовать документ для компьютера — значит, определить, из каких именно тем состоит его «тематическая смесь» и в каких пропорциях ее «смешали» в конкретном тексте. Но сначала придется еще решить, сколько всего должно быть тем и из каких слов они состоят.
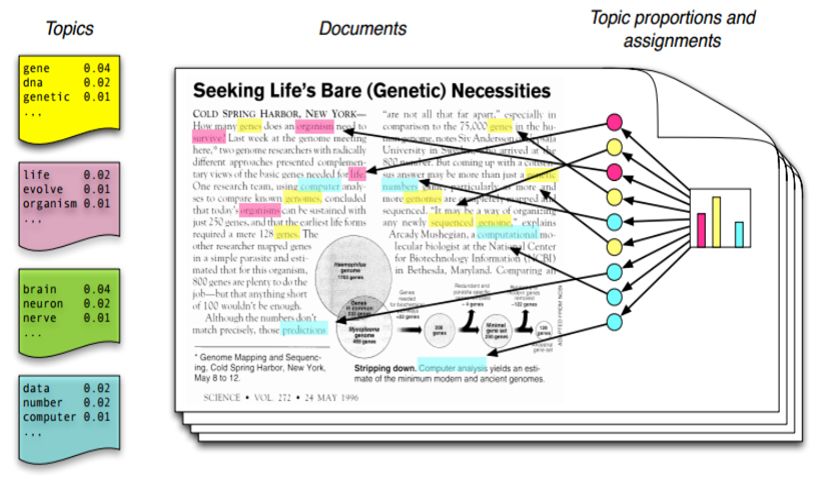
Способ первый — LSA
LSA — это «латентно-семантический анализ». Его суть состоит в том, чтобы:
- Показать в таблице, как часто все слова встречаются в документах
- Переупорядочить таблицу так, чтобы слова одной темы и документы похожих тем стояли рядом
Сначала разберемся, что это за таблица встречаемости. Как мы помним, алгоритм работает не с одним документом, а с несколькими, причем на разные темы. Итак, столбцами таблицы сделаем все документы по порядку, обозначим их d1, d2, d3 и так далее. Строками таблицы станут термины из словаря по алфавиту: Абакан, абажур, и т.д до последней буквы. Каждая ячейка таблицы сейчас показывает, сколько раз данное слово встретилось в данном документе. Каждый столбец отображает, какие слова встретились в документе, а каждая строка — наоборот — в каких документах встретилось слово.
В этой таблице нет цифр, потому что записывать в ячейки абсолютные значения встречаемости слов не очень полезно. Бывают стоп-слова, они практически ничего не означают, не относятся к темам и, тем не менее, встречаются часто почти во всех текстах. Слово «ядерное», например, явно даст больше знаний о теме документа, чем слово «испытание», так как «испытание» встретилось еще в десятке текстов, никак не связанных с ядерной физикой, это скорее стоп-слово.
Идею о том, что некоторые слова сильнее других «оттягивают» документ к своей теме, можно выразить численно. Поэтому на самом деле в таблице встречаемости вместо чисел «слово X нашлось в документе Y пять раз» записывают показатель, названный tf-idf (на картинке — чем показатель больше, тем темнее ячейка). Вот, как он рассчитывается:
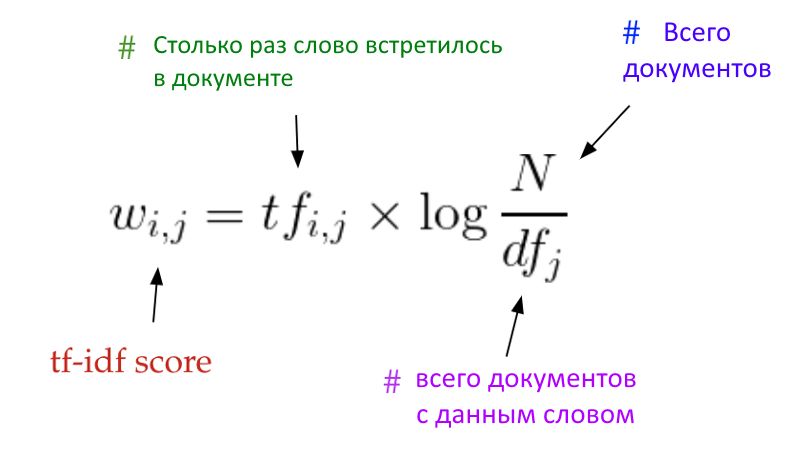
Вкратце — значение tf-idf возрастает, если термин часто встречается в пределах одного документа и при этом редко — во всей коллекции. Тогда исследователь решает, что нашел важный для тематической классификации термин, который означает что-нибудь специфическое.
Теперь перемешаем строки и столбцы таблицы
Итак, мы получили матрицу, учитывающую вес слов в составе документов. Эта матрица будет беспорядочной и разреженной (т.е. состоящей в основном из нулей — ведь большинство слов встречается в 1-2-3 документах из тысячи). По ней трудно сделать выводы о темах. Чтобы делать выводы, нужно как-нибудь упорядочить таблицу.
Для этого хорошо подходит метод из линейной алгебры, он называется сингулярным разложением матрицы, сокращенно — SVD. Этот метод позволяет приближенно представить матрицу в виде произведения трех других матриц, называемых U, S и V. Если в V поменять местами столбцы и строки, ее имя можно записать как V^T (читается «транспонированная V»).
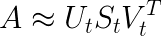
При этом у каждого из получившихся множителей есть полезные свойства, связанные с поиском тем.

На картинке выше A’ — исходная беспорядочная матрица, представленная как произведение трех других матриц. Самая важная из них — средняя матрица S. По главной диагонали слева направо в ней идут специальные числа, а остальные значения — нулевые, как на картинке ниже:
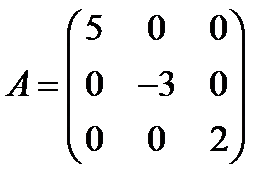
Специальные числа из S называются сингулярными. Сингулярным числом матрицы число называется тогда, когда существует два вектора («левый» и «правый» сингулярные векторы) — один совпадает по числу элементов с шириной исходной матрицы, другой — с ее высотой. При этом длина векторов равна единице, а если умножить матрицу на один из них, то получится то же самое, как если бы мы умножали второй вектор на сингулярное число σ (сигма).
Матрицы U и V состоят из левых и правых сингулярных векторов соответственно. Из-за свойств сингулярных чисел эти матрицы являются унитарными. Это значит, что если строки в них записать в столбик, а столбцы — в строку, а потом умножить старую матрицу на новую, то получится матрица, где все элементы, кроме единиц на главной диагонали, равны нулям. Ниже — примеры единичных матриц, они получаются, если умножить U или V на собственную зеркально отображенную версию.
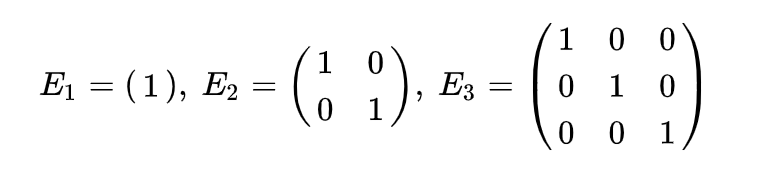
В общем, полезная часть для нас состоит в том, что колонны в матрицах U и V соответствуют темам в тексте, которых в общей сложности t штук. Чему равно t — человек задает вручную при вычислении разложения, а значит, всегда есть возможность найти ровно t тем. Математически это представлено так, что алгоритм разложения выбирает из исходной матрицы t самых больших сингулярных чисел и формирует из них среднюю матрицу S, элементы которой идут по диагонали.
Колонны в U и V соответствуют темам, но что выражают строки? Строка матрицы U — это документ, выраженный через темы (колонны); а в V строки соответствуют отдельным словам из словаря. Следовательно, первая строка матрицы U показывает, какие темы встречаются в первом документе коллекции, а первая строка V показывает, к каким темам относится первое слово из словаря.

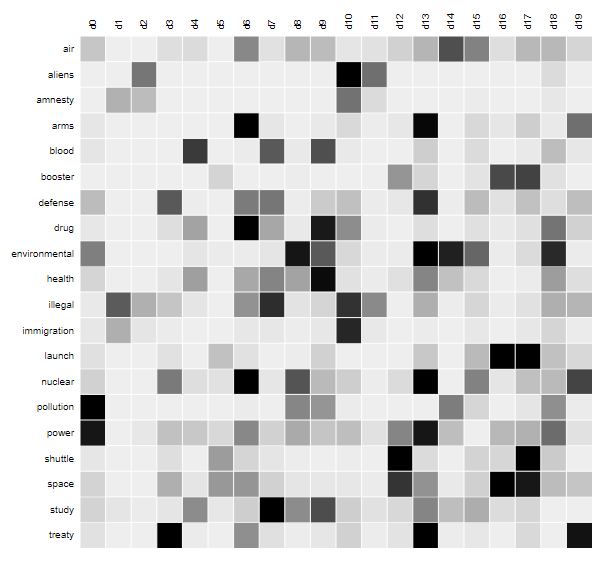
Так LSA выглядит в движении: используя матрицы-множители, где документы и слова выражены через темы, алгоритм группирует документы, где встречаются одни и те же термины, а затем — слова, найденные в одних и тех же документах. Получающиеся «островки» как раз являются тематическими кластерами — к первой теме относятся слова air, pollution, power, environmental, ко второй — illegal, international, amnesty, aliens. Документы, в которых встречаются похожие термины, машина теперь сможет объединить в категорию — при том, что вручную в нее никто не загружал знания о том, что существуют темы, контексты и смыслы. Свой вывод программа сделала потому, что нашла в нескольких документах одни и те же слова.
Способ второй: вероятностный LSA, или pLSA
Сначала немного про теорию вероятностей. Математики придумали формулы расчета вероятности наступления взаимосвязанных событий. Если подбрасывать монетку и считать вероятность, что выпадут две решки подряд, подобная формула не нужна: новый бросок монеты не связан с предыдущими. Вероятность наступления первого И второго независимых событий — произведение их вероятностей. ½ (выпала первая решка) * ½ (выпала вторая решка) = ¼ (выпали две решки подряд).
Но в жизни события связаны друг с другом. Обычно бывает так, что мы делаем какие-то наблюдения и предполагаем, что между тем, что случилось в прошлом, и тем, что наступит в будущем, есть зависимость. Хотя бы потому, что некоторые из прошлых событий отсекают часть будущих вариантов (например, для случайного жителя Земли вероятность умереть от рака простаты довольно высока; но если вы родились девочкой, эта вероятность равна 0).
Эту связь учитывает формула условной вероятности. Она поможет предугадать слово в документе по предыдущему контексту, рассчитать вероятность действий человека по его предыдущим поисковым запросам, сделать еще много всего интересного. Вот так записывается условная вероятность: P (E|F).
Читается как «вероятность наступления события Е при условии, что уже наступило событие F». То есть формула читается в некотором роде справа налево: сначала наступает F, мы узнаем об этом, и на основе полученного знания делаем вывод о вероятности E. Например, событием E может быть появление в тексте слова «котик». А событием F — появление какого-нибудь другого слова перед словом «котик». Тогда если мы посчитаем вероятности на большом наборе текстов, то условная вероятность появления «котика» P (E|F) при F = «пушистый», например, окажется выше, чем вероятность P (E|F) при F = «помидорный». Слово «пушистый» повышает шансы читателя встретить далее слово «котик».
Так вот, сама формула условной вероятности, формула Байеса, выглядит так: ¨P(E|F) = P (E, F) / P (F)«. Она означает, что для расчета вероятности события E при условии события F нужно разделить вероятность события «наступило E и F вместе» на вероятность F, т.е. на вероятность выполнения условия«. Звучит сложно, но без паники! Вот простой пример:
В семье живут два ребенка. Мы не знаем их пол, но при этом пол одного не зависит от пола другого. Какова вероятность того, что оба ребенка — девочки? ¼ — потому что события сейчас независимы, как в случае с монетками.
Теперь добавим связи. Есть два события: старший ребенок — девочка (событие G) и оба ребенка — девочки (событие B) Какова вероятность того, что оба ребенка — девочки P(B), если известно, что старшая — точно девочка P(G)? То есть какова вероятность события B при условии G, P(B|G)? Здесь удобно показать на таблице.

Вариантов, где старший ребенок — девочка — два из четырех (верхняя строчка). Значит, вероятность выполнения условия, что старший ребенок — девочка, P(G) = ½. По формуле условной вероятности P(B|G) = P (B, G) / P(G). Значит, осталось узнать вероятность P(B, G), то есть вероятность того, что оба ребенка — девочки и при этом старший ребенок — девочка. Оба ребенка — девочки только в одном случае из четырех в таблице. Вероятность P(B, G) = ¼. Значит, P (B, G) / P(G) = ¼ : ½ = ½. Вероятность того, что оба ребенка — девочки, если старшая — девочка — ровно половина. Это легко предположить и без формулы условной вероятности, ведь если мы знаем пол старшего ребенка, то младший может быть либо девочкой, либо мальчиком с равной вероятностью.
А теперь интересная часть, где формула условной вероятности все-таки пригождается. Какова вероятность, что оба ребенка — девочки, если хотя бы один из детей (а не точно старшая) — девочка? Ответ будет уже другим — ⅓! Как это вышло?
Итак, снова нужно найти вероятность события L (обе — девочки) при условии события K (хотя бы один ребенок — девочка). P(L|K) = P (L, K) (событие И условие) / P (K) (условие).

Какова вероятность K? Случаев, когда хотя бы один ребенок — девочка — 3 из 4 на картинке. P(K) = ¾. А какова вероятность того, что оба ребенка — девочки и при этом хотя бы один из них — девочка? Обе девочки может быть только в одном случае из четырех, ¼. Так что вероятность наступления первого и второго события в данном случае сводится к вероятности наиболее редкого из них. Поэтому P(L, K) = ¼. Значит, наконец, чтобы рассчитать условную вероятность P(L|K), разделим ¼ на ¾ и получим ⅓ — вероятность того, что дети окажутся двумя девочками, если хотя бы один из детей — точно девочка.
А почему условная вероятность важна для тематического моделирования?
Вспомним базовое предположение LSA: документ состоит из смеси тем, а каждая тема — это коллекция слов.
Вероятностный LSA, или pLSA (где «p» значит «probabilistic», «вероятностный») предполагает, что текст можно генерировать, случайно выбирая слова. Делаются следующие допущения:
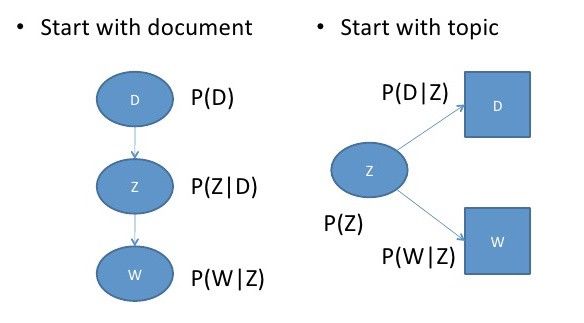
Если имеется документ D, то тема Z в ней представлена с условной вероятностью P(Z|D)
Слово W встречается в теме Z с вероятностью P(W|Z)
Именно эти вероятности и нужно определить для каждого слова, темы и документа. Построить тематическую модель коллекции документов D — значит найти множество тем Z, распределения слов по темам P(W|Z) и распределения тем по документам P(Z|D).
Представим для наглядности, что при написании текста фокусник достает карточки со случайными словами из нескольких тематических шляп. Каждая шляпа отвечает за одну тему. Фокусник из pLSA знает, какие темы бывают в конкретном документе, и на этой основе он сначала наугад выбирает одну из подходящих шляп. Потом он выбирает случайное слово из тематической шляпы и складывает в одну из стопок перед зрителями: каждая стопка — отдельный документ. Порядок слов не важен, важен только состав.

Так pLSA представляет процесс порождения документов, если уже известно, с какой вероятностью тема встретится в документе, а слово — в теме. То есть — с какой вероятностью фокусник выбирает конкретную шляпу и в ней — конкретное слово. Но на самом деле это заранее неизвестно, что и предстоит выяснить алгоритму. Условная вероятность здесь нужна как раз затем, чтобы описать событие «выбрано слово „морковь“ при условии выбора темы „овощи“ при условии, что эта тема есть в документе „О вкусной и здоровой пище“».
Если описывать более формально, то
- При условии выбора документа D выбирается тема Z с вероятностью P(Z|D)
- При условии выбора темы Z выбирается слово W с вероятностью P(W|Z)
А значит, математически вероятность встретить данное слово и данный документ вместе (то есть слово в документе) равна произведению вероятностей отдельных событий (знак Σ (сигма) в означает, что мы посчитаем произведение для каждого возможного Z и сложим их):
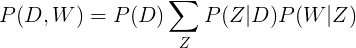
Правая часть выражения говорит нам, насколько вероятно встретить определенный документ из коллекции, а на основе распределения тем в документе — насколько вероятно встретить в документе конкретное слово.
Сейчас множители P(D), P(Z|D), и P(W|Z) — параметры тематической модели. P(D) — вероятность выбрать конкретный документ из всех — можно наблюдать напрямую из коллекции документов, а P(Z|D), и P(W|Z) моделируются в виде полиномиальных распределений при помощи алгоритма максимизации ожидания. Вкратце — этот алгоритм формирует функцию и подбирает к ней самые вероятные параметры, основываясь на наблюдениях, в нашем случае — подбирает вероятность встретить ту или иную тему. Представьте, что вы приехали в незнакомый город и увидели работающий фонтан на площади. Вы можете предположить, что фонтан работает ежедневно, или предположить, что он работает раз в год и вы случайно попали именно в тот день, когда фонтан работает. Первое предположение вероятнее, и вы остановитесь на нём. По такому же принципу моделируются параметры P(Z|D) и P(W|Z).
Еще интересно, что вероятность встретить слово в документе P(D, W) можно составить иначе:
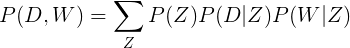
Сравните с предыдущим вариантом:
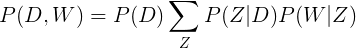
То есть сначала мы выбирали документ D, из него — тему с учетом документа (Z|D), потом слово с учетом темы (W|Z). В новом уравнении мы начинаем с выбора темы и независимо выбираем документ с учетом темы (D|Z) и слово с учетом темы (W|Z).
Так можно сделать, если заранее условиться, что появление слов в документе D, относящихся к теме Z, описывается общим для всей коллекции правилом и не зависит от конкретного документа D.
Так вот, причина, по которой новое уравнение так интересно — в том, что между ним и старыми разложением матрицы A на три другие матрицы U, S и V можно увидеть параллель:
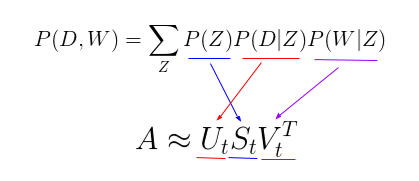
Вероятность встретить данную тему P(Z) соответствует матрице с сингулярными числами S, вероятность найти документ с учетом выбранной темы — тема-документной матрице U, а вероятность встретить слово в теме — матрице V.
О чем это говорит? Хотя новые формулы выглядят иначе и подходят к решению проблемы совсем с другой стороны, на самом деле pLSA просто рассматривает те же самые процессы с точки зрения теории вероятности. У pLSA есть свои минусы, и обычно этот метод не используется отдельно. Куда популярнее — LDA.
Способ третий, LDA
LDA расшифровывается и переводится как «латентное размещение Дирихле» и в своей основе полагается на распределение вероятностей Дирихле. Что это такое?
Обычное распределение вероятностей, например, нормальное распределение, показывает, насколько вероятно наугад выбрать одно из разрешенных значений.
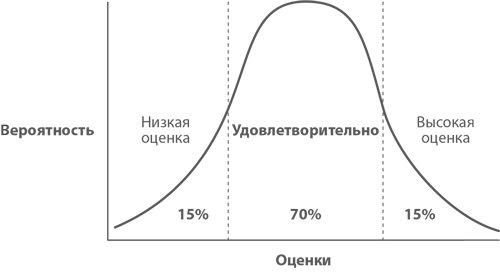
Распределение Дирихле идет на ступень выше — показывает, насколько вероятно выбрать одно из разрешенных распределений значений. Покажем на примере.
Допустим, есть MMORPG, где очки навыков можно вкладывать в силу, скорость или выносливость. Пусть каждый из навыков будет вершиной треугольника. Координаты «выносливости» пускай будут (1, 0, 0), «силы» — (0, 1, 0), «скорости» — (0, 0, 1).
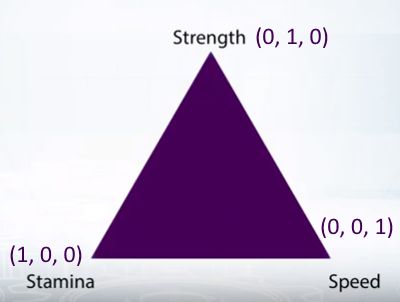
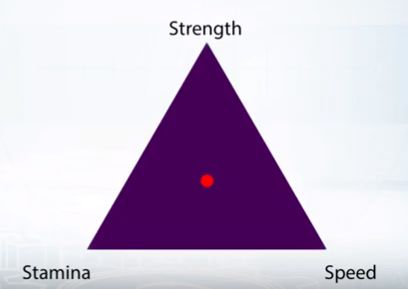
Теперь допустим, что какой-то игрок чаще вкладывал очки опыта в выносливость или скорость. То, как он это делал, показано точкой на картинке.
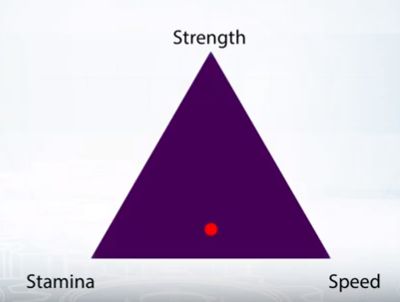
Наверное, он и дальше будет распределять очки опыта с вероятностью примерно (0,8; 0,2, 0,8) — чем дальше точка от вершины, тем ниже вероятность вложить очко в данный навык. Эта точка — распределение вероятностей. Одно из возможных распределений. Но могут быть и другие:
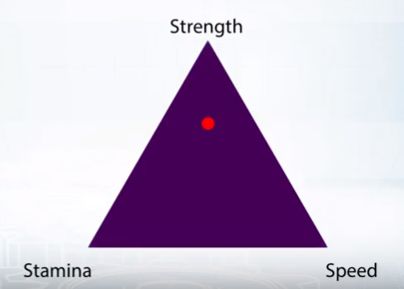
Например, если игрок прокачивал силу (0,2; 0,8; 0.2).
Или если одинаково вкладывался во все навыки (0,5; 0,5; 0,5).
Так вот, если собрать статистику по всем игрокам и посмотреть, как они тратили очки навыков, мы получим области, где чаще всего может встретиться точка, и области, где она может встретиться реже. Иными словами, мы получим распределение вероятностей получить то или иное распределение вероятностей.
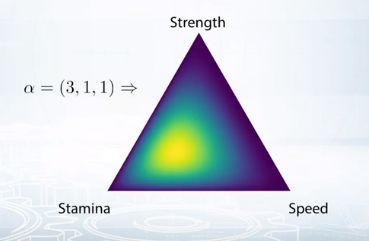
Именно это «распределение распределений» — и есть распределение Дирихле. В данном случае игроки чаще тратили очки опыта на выносливость, и вероятность встретить их точку возле этой вершины треугольника выше среднего.
А когда речь идет о тематическом моделировании, распределение Дирихле предсказывает, какими именно могут быть распределения вероятностей встретить тему в документе или слово в теме, если известно, каким в теории может быть это распределение. В pLSA мы напрямую выбирали документ d, из него — тему z, а из темы z — слово w. В LDA все немного иначе. Вот так вещи обстояли в pLSA, когда мы генерировали документ:
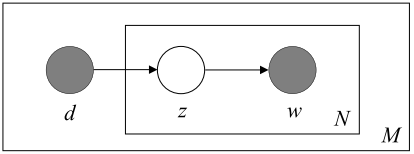
А вот так — в LDA:
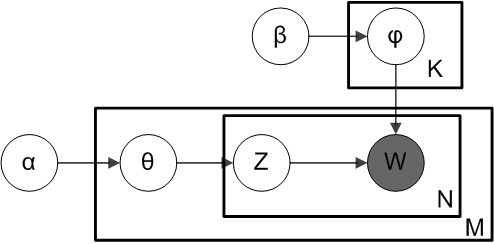
На основе заготовленного распределения Дирихле Dir(α) мы выбираем наиболее вероятное распределение тем в документе — θ (тета). На основе распределения тем θ выбирается уже конкретная тема Z.
Затем на основе другого распределения Дирихле — Dir(𝛽) — выбирается самое вероятное распределение слов в теме Z, это распределение слов называется φ (фи). Из φ мы напрямую выбираем слово W.
То есть распределения Дирихле Dir(α) и Dir(𝛽) можно сравнить с областями, где наиболее вероятно встретить конкретные точки φ и θ. В свою очередь, каждая из точек обладает координатами, только их не три, как в примере с игрой, а столько, сколько слов в теме для φ или тем в документе для θ.
Теперь, допустим, мы подали на вход алгоритму LDA документ. Программа уже знает, как математически описать функцию генерации документа и сможет подобрать к ней конкретные переменные (то есть распределения тем и слов внутри них) так, чтобы результат воображаемой генерации был похож на поданный на вход документ. Так LDA определит состав тем и их распределение по документу, ничего заранее не зная о тексте.
К тематическому моделированию существует много подходов. Все их объединяет тот факт, что текст для компьютера — это набор численных показателей о встречаемости тех или иных слов, о вероятности их появления. Чтобы сделать вывод о том, что два текста затрагивают одну и ту же тему, нужно найти в них одни и те же слова — для этого не нужен философ, который объяснил бы, какие вообще темы бывают в текстах. Вот так с помощью несложных в своей основе идей тематическое моделирование немного приближает момент, когда вычислительная машина сможет «понимать» речь почти по-человечески.
Источники:
- Тематическое моделирование с LSA, pLSA, LDA
- Анимация LSA в движении
- Вероятностное тематическое моделирование — К.В. Воронцов
- Интуитивное объяснение распределения Дирихле
- Что такое распределение Дирихле? (видео)


