Нейросети сегодня используют везде. Они помогают «умной» видеокамере распознать лицо, банкомату — цифры на чеке, а гугл-переводчику — найти на картинке слово и верно перевести его.
Всем хочется найти понятное объяснение того, как работают нейросети, но в интернете обычно рассказывают либо слишком сложные вещи, либо очевидные. Мы попытались доступно изложить базовые идеи, стоящие за созданием нейронных сетей. Статья не претендует на полноту и абсолютную научную точность. Зато мы постарались быть понятными.
© vas3k
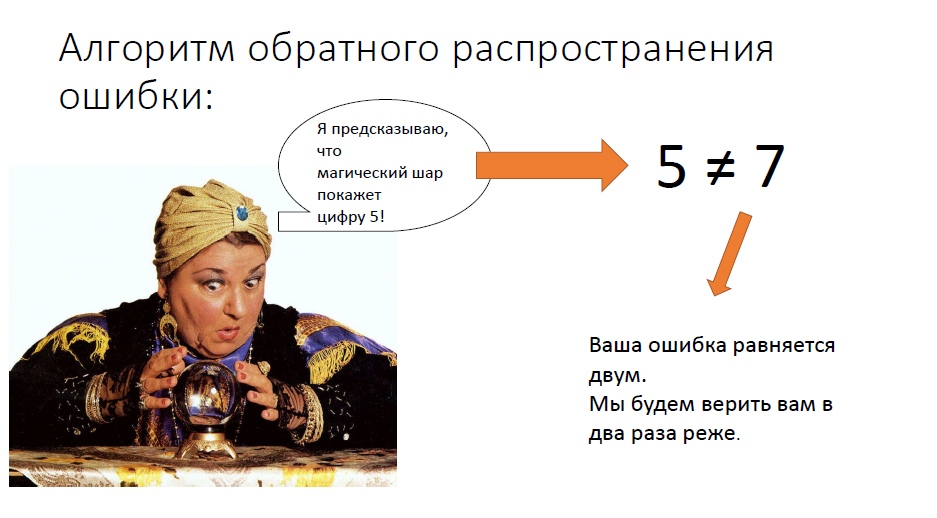
Нейросеть — это обучаемая система. Она действует не по заданным правилам, а на основе прошлого опыта. Как нейросети получают опыт? При помощи алгоритма обратного распространения ошибки. Сначала нейронная сеть делает предсказание какого-нибудь значения, а затем предсказание сравнивается с истинным (в нашем примере истинное значение на клавиатуре пускай вводит программист: так будет проще). Вычисляется разность между предсказанным и истинным значением — это величина ошибки. На втором шаге устройство нейросети корректируется так, чтобы в следующий раз уменьшить ошибку.
Как это работает?
Еще в сороковые годы учёные подумали: если мы хотим создать искусственный интеллект, почему бы не «срисовать» его устройство с человеческого мозга? В биологии нейронами называют нервные клетки, способные хранить, получать и передавать электрические импульсы по специальным «усикам» — аксонам и дендритам. У нейрона много дендритов, они «приносят» импульсы, а аксон всегда один, и он «уносит» импульсы от нейрона.
Искусственная нейросеть тоже состоит из нейронов. Чтобы было проще, договоримся, что искусственный нейрон в компьютере — это просто некая воображаемая чёрная коробка, у которой много входных отверстий и одно выходное (как аксон и дендриты, помните?). Как выходной сигнал формируется из кучи входных — определяет внутренний алгоритм нейрона.

Чтобы разобраться, опишем небольшую программу, которая будет распознавать простые изображения, скажем, картинки с цифрами.
В исходном состоянии наша система будет иметь «пустую» память. Этакий новорожденный мозг, готовый к бою. Чтобы заставить его корректно работать, нам нужно будет потратить время на обучение. Мы подаем на вход программе какие-то данные, а у нее есть какие-то варианты «ответа» нам.
Сколько вариантов выхода может быть в задаче распознавания (арабских) цифр? Правильно, столько же, сколько символов мы будем уметь определять, а именно — 10 (ноль тоже считается).

Определимся со входными данными. Давайте будем подавать на вход маленькие черно-белые картинки размером 3 на 5 пикселей. Программа будет их видеть немного иначе — как набор нулей и единиц. На месте черного пикселя — 1, на месте белого — 0 (примерно как пятерку на картинке ниже).

В конце распознавания у нас будет набор нейронов, каждый из которых пытается найти конкретную фиксированную цифру. Он считает, что нашел цифру, и что он прав на сколько-то процентов. Чем больше процент, тем вероятнее, что именно этот нейрон прав на самом деле.
Для работы нам нужно где-то хранить предыдущие результаты, память нейрона, позволяющую ему обучаться, например — в картинке 3×5, какую мы подаем на вход. Для примера, так выглядит визуализация памяти нейрона, распознающего букву «К» после прогона более сложной программы по разным шрифтам (эта нейросеть распознает не цифры, а буквы):

Самые насыщенные области соответствуют наиболее часто встречающимся пикселям.
Итак, на вход мы будем подавать изображение, поэтому входные данные представляют собой табличку пикселей. Каждый пиксель картинки на входе может быть либо черным (1), либо белым (0).
Теперь раскроем магию черного ящика: внутри него происходит простое математическое преобразование. Входные переменные (1 — черный пиксель, 0 — белый пиксель) умножаются на специальные числа, называемые весами.
Все полученные произведения складываются. Важно, что результат умножения каждого пикселя на вес попадает в память нейрона. Например, если пиксель был черным (подал на вход 1), он умножается, скажем, на 3, то 3 попадает в память нейрона. А если был белым — на 3 умножаем 0 и получаем 0: белый пиксель не оказал влияния на сумму произведений. Чем больше множитель (вес) — тем сильнее (важнее для нейрона) сигнал.
Если полученная сумма превосходит некое заранее заданное число, нейрон считает, что нашёл на картинке свою цифру. «Вес» может быть отрицательным: если пиксель с таким весом оказался черным, от суммы, наоборот, отнимаем 3, а не прибавляем ее.
Резонный вопрос: как определить «веса» пикселей? Это самый важный вопрос: именно расстановкой и коррекцией весов и занимается нейросеть во время обучения. Именно с помощью подбора весов нейросеть постепенно запоминает, какие части данных важны, а какие — нет. Давайте рассмотрим, как обучается нейрон, пытающийся «узнать» единственную цифру 5.

Программа будет говорить нам, является скормленная ей картинка изображением цифры 5 или нет, то есть на выходе получаем простой ответ: «Да» или «Нет».
Расплата за ошибку
Если нейрон выдает правильный ответ — радуемся и ничего не делаем. А если ошибается — наказываем его. Если получен ответ «Нет» (т.е. цифра не найдена, хотя она на картинке есть) — прибавляем значения входов к весам каждого пикселя. Если ответ «Да» (т.е. нейрон говорит, что цифра найдена, хотя ее на картинке нет) — вычитаем значения входов из веса каждого пикселя.

Представим, что текстовый файл, заполненный нулями 3×5 — это чистая память нейрона, начальные значения весов каждого пикселя:

Загружаем на вход картинку цифры 5:

Программа сравнивает с собственной памятью эту комбинацию, но в каждом случае, где точка оказалась черной, единица на входе умножится на ноль. Сумма нескольких ноликов равна нулю, так что программа выдаст на выход ответ «Нет». Это неверно, поэтому к каждому пикселю, где были черные точки (которые вместе составляют цифру 5), прибавляем «вес» 1 и обновляем сохраненную память. Вот, что получится:

Теперь чувствительность входов, где были черные точки, повысилась, а память программы обновилась. Она как бы один раз запомнила, как выглядит пятерка. В следующий раз, если загрузить ей ту же картинку, она распознает ее. Но теперь мы усложним задачу и будем подавать разные цифры.
После долгих попыток обучения нейрона по распознаванию картинки с цифрой 5 его память станет выглядеть примерно вот так:

Самое интересное в этой картинке — две точки со значением веса −4: если пиксели в этих местах черные, программа сразу теряет уверенность в том, что видит перед собой пятерку. Почему? Потому, что существуют цифры 6 и 9, которые похожи на пятерку вплоть до двух пикселей — как раз тех, что получили отрицательные значения.
Программа, получив на вход 6 или 9, то есть набор всех пикселей для пятерки и один лишний, сложила значения их весов, и сумма превзошла нужную — а значит, выдала ложное срабатывание. А это, как вы помните, ведет к понижению весов всех входных пикселей. Веса всех других пикселей в процессе обучения восстановились, а этих двух — нет: программа «запомнила», что в этой части картинки искать пятёрку не нужно.
Источники:
- Deep Visualisation Toolbox
- Habr: Нейросети для чайников. Начало.
- Habr: Нейросети для чайников — Перцептрон.