Этот пост о технологиях компьютерного зрения мы решили разбить на две части: в первой — рассказываем о том, как устроены графические фильтры и что с их помощью можно делать с изображением. Во второй — объясняем, как полезные свойства фильтров помогают нейросетям обрабатывать картинки.
Мы привыкли, что в ВК, в Фейсбуке или в Инстаграме можно за пару секунд наложить фильтр на изображение: размыть его, подправить цвет, яркость, контрастность, добавить какие-то пятна. Звучит удивительно, но в своей основе фильтр размытия в Инстаграме и сверточная нейросеть работают одинаково. Как?
Коротко: умножают значения пикселей на картинке на специальные числа
Когда картинка состоит из пикселей, у каждого пикселя есть координаты и число, однозначно кодирующее его цвет. А значит, это число можно с чем-нибудь сложить или на что-нибудь умножить.
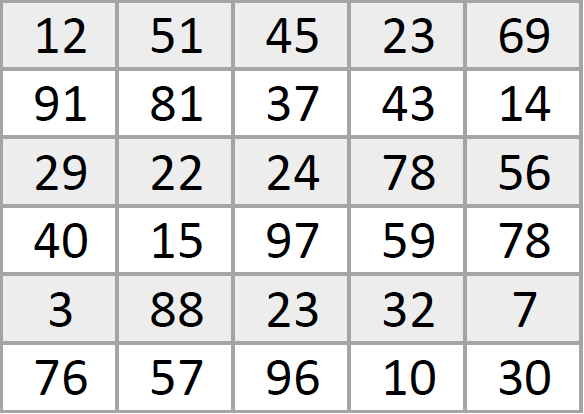
Давайте представим, что вот это наша картинка: каждая ячейка таблицы — это один пиксель, а числа обозначают их цвета.
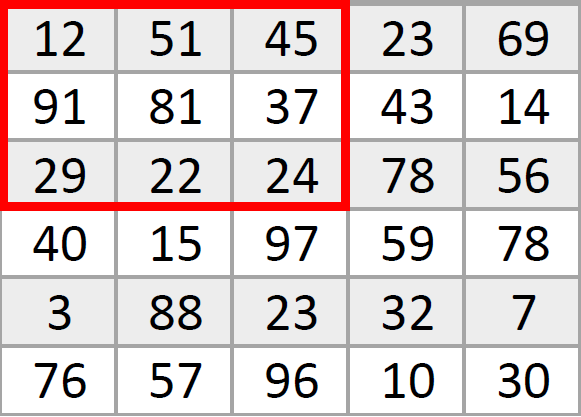
Сейчас будем размывать картинку. Для этого возьмем в красную рамочку девять пикселей в верхнем левом углу, посередине будет 81. Вот так:
Помните, что мы собирались умножать значения пикселей на специальные числа? Время пришло. Наши числа пока простые. Возьмем «рамку» из девяти единиц и умножим каждый пиксель в красной рамке на единицы из соответствующих ячеек, как на гифке.
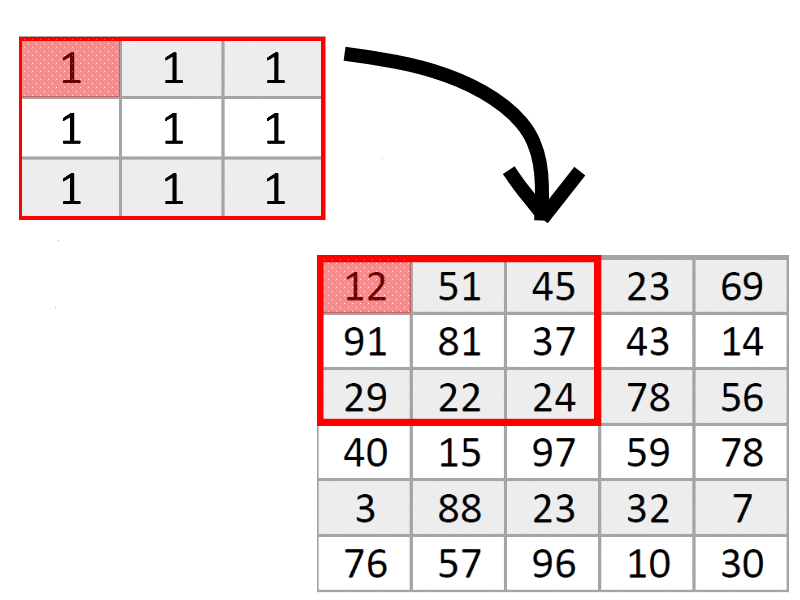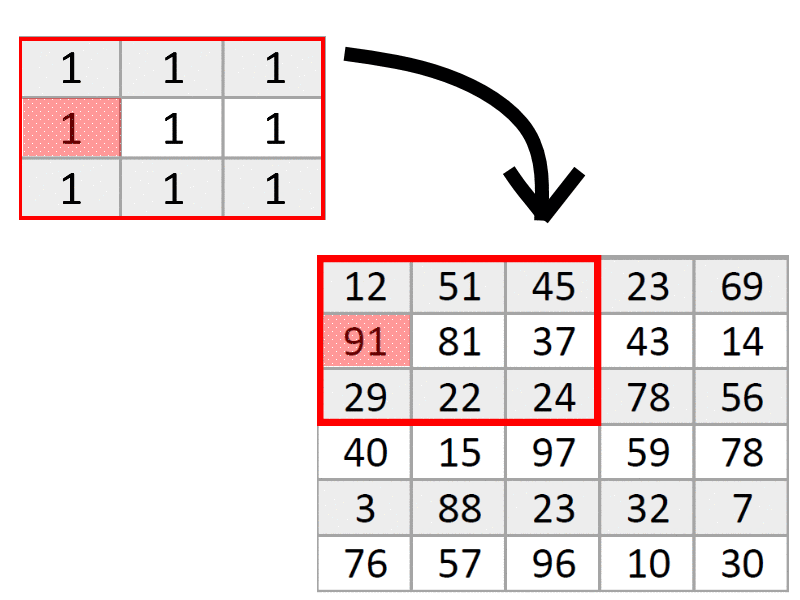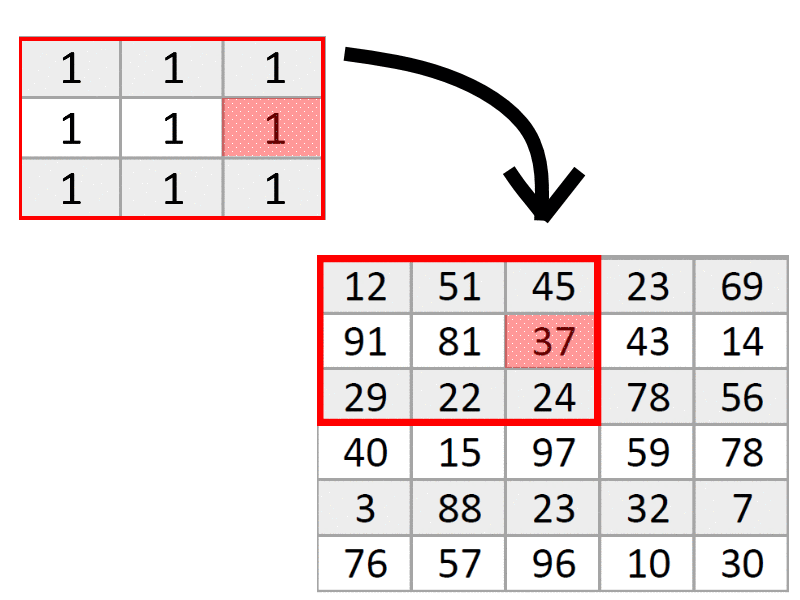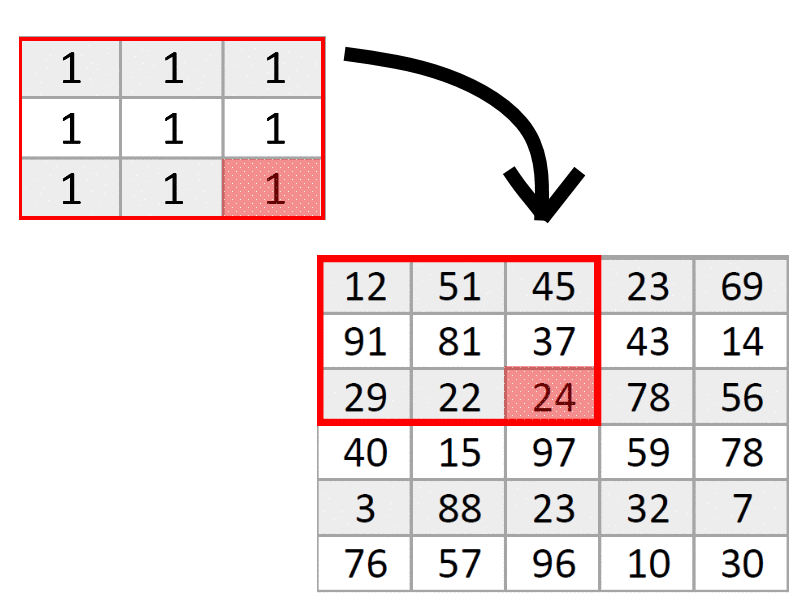
От умножения на единицу числа не изменятся, но это нам пока и не нужно. Любой фильтр сначала умножает пиксели с большой картинки на значения из маленькой «рамки», а потом находит среднее арифметическое всех произведений и записывает результат вместо того пикселя, который был посередине рамки, в нашем случае, вместо 81 напишем 43. Именно пиксель, оказавшийся посередине маленькой рамки — самый главный, это его значение в конечном итоге изменится, и ради него мы создавали маленькую рамку. По сути, поскольку в рамке были одни единицы, мы просто нашли среднее арифметическое цветов всех пикселей в рамке.
Хорошо, мы выделили какой-то пиксель и перекрасили его в «средний цвет» пикселей вокруг него. Что дальше?
Коротко: сделать то же самое для всех остальных пикселей.
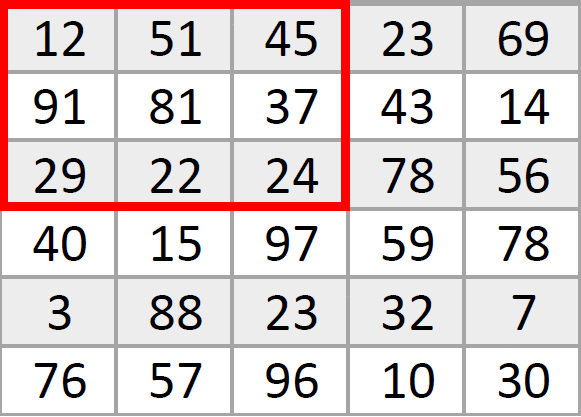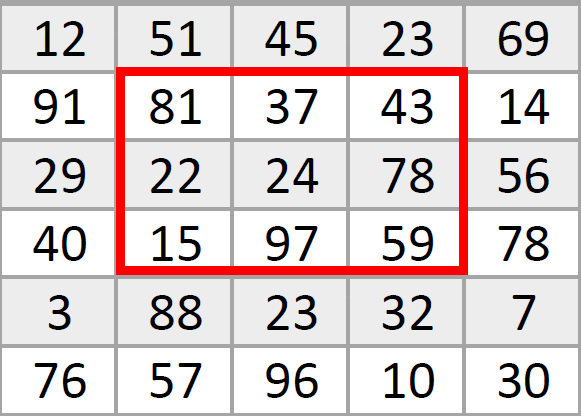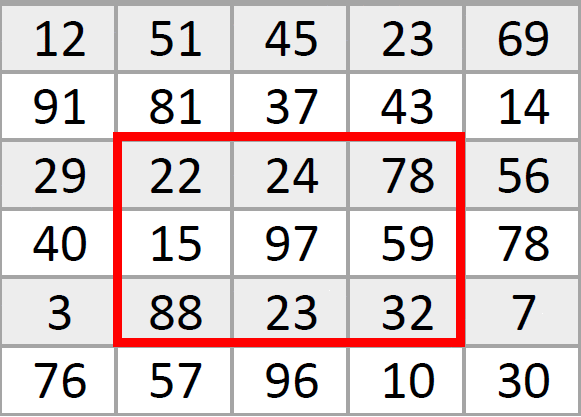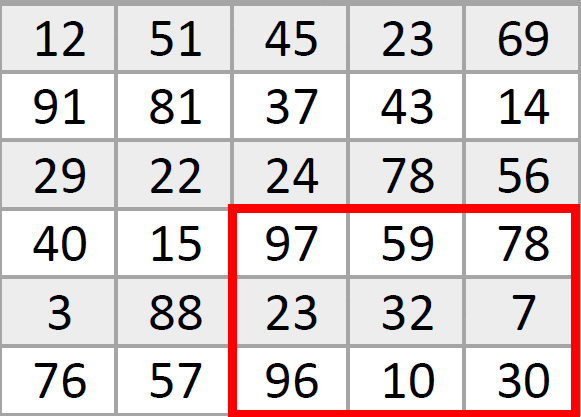
Вот так маленькая «рамка» по очереди «пробегает» по всем пикселям большой картинки, за раз изменяя значение только одной точки посередине. Кстати, новое значение пикселя в центре рамки записывается в новую картинку, чтобы не сбивать алгоритм изменяющимися числами. Если рамка должна обработать пиксель на краю изображения, тут уже разработчики сами решают, стоит ли дорисовать новые точки вокруг него или обойтись анализом только тех, что уже «есть в наличии».
Для того чтобы каждый раз не писать, что «нужно умножить числа из таблицы на числа из рамки», математики придумали называть эти таблицы матрицами, их можно складывать и умножать. Маленькая красная рамка, которая умножает несколько пикселей на специальные числа, а потом суммирует результаты — на самом деле матрица, и она называется ядром свёртки. Процесс «пробегания» ядра свёртки по пикселям изображения составляет суть операции свёртки. Эту операцию свёрточная нейронная сеть проделывает на каждом из своих свёрточных слоёв, отсюда и название.
Если в ядре свертки одни единицы, то такое ядро перекрашивает центральный пиксель буквально в среднее арифметическое цветов его соседей. То есть точка, выбивающаяся из окружения, поблекнет и «перекрасится» под его цвет. Это может быть полезно, когда нужно убрать шум с фотографии, а мы «бегаем» по картинке рамкой 3×3 пикселя, выбирая только нужные, слишком яркие точки.
Но если применить усреднение к большому участку цветной фотографии, то каждый из пикселей внутри рамки окажет равное влияние на итоговый цвет, и все цвета перемешаются.
Вот пример: так изображение выглядит до применения фильтра:

Попросим компьютер усреднить значения пикселей:
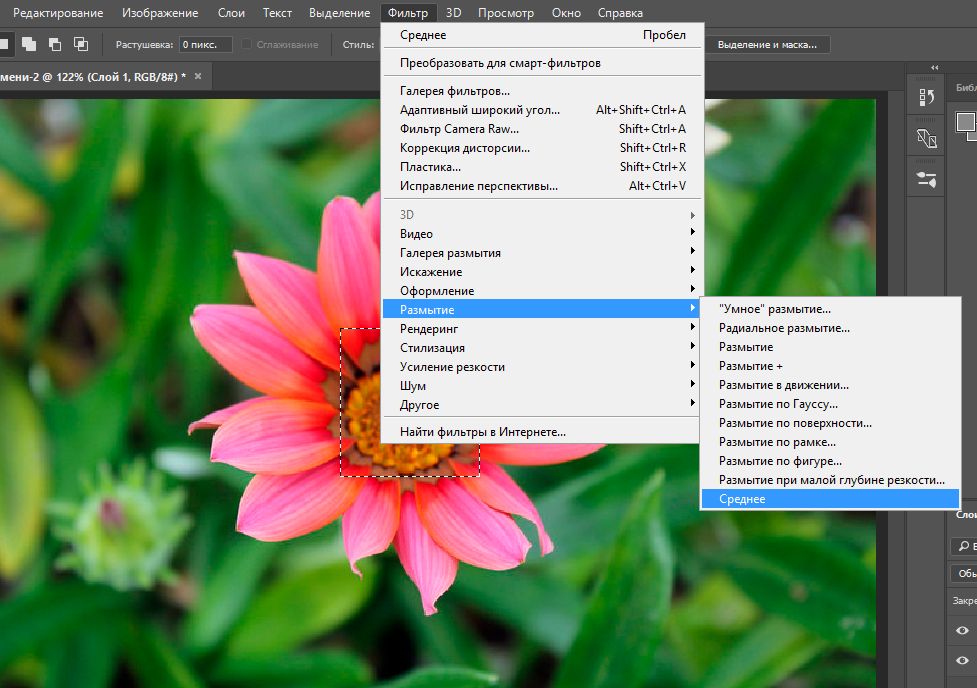
Вот, что получится:

На иллюстрациях видно, что настолько радикальное размытие совсем «сломало» текстуру картинки. Значит, нужно придумать способ так размывать её, чтобы какие-то пиксели оказали больше влияния на результат, чем другие, что сохранит неоднородную текстуру (и позволит действительно убирать шум, а не перекрашивать всё одинаковым цветом). Как это сделать?
Сейчас будем придумывать, на что еще, кроме единиц, можно умножать значения пикселей.
Множители в ядре свёртки можно воспринимать как вес, значимость сигнала, передаваемого тем или иным пикселем. Ведь если умножить значение пикселя на 4, он окажет больше влияния на сумму произведений, чем если бы его умножали на единицу. Ядро, кстати, не обязательно должно быть таким маленьким, его размер не ограничен. И было бы логично, если бы при размытии картинки большее влияние на цвет пикселя, который мы сейчас перекрашиваем, оказывали бы его соседи, а не более далекие точки.
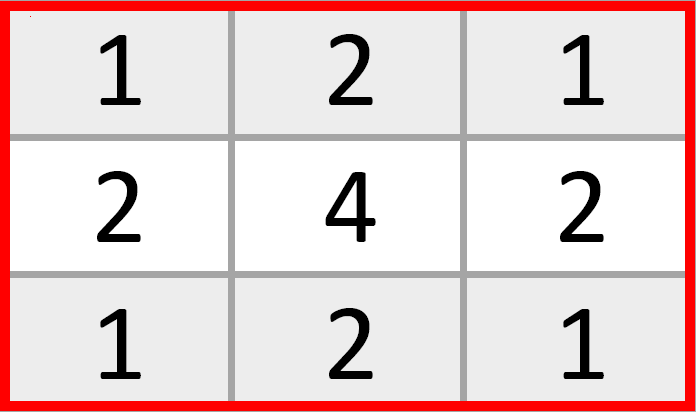
Например, если распределить веса (множители) в ядре свертки так, как показано на рисунке, получится Гауссово размытие — операция, знакомая многим по Фотошопу. Гауссово оно потому, что множители расставлены как на графике—»колоколе» гауссовой функции: посередине большие значения, по краям — маленькие.
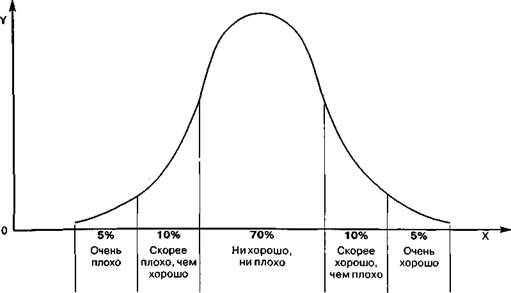
А еще эта рамка научит компьютер определять, где на картинке заканчивается цветок и начинается фон, главное — правильно расставить коэффициенты.
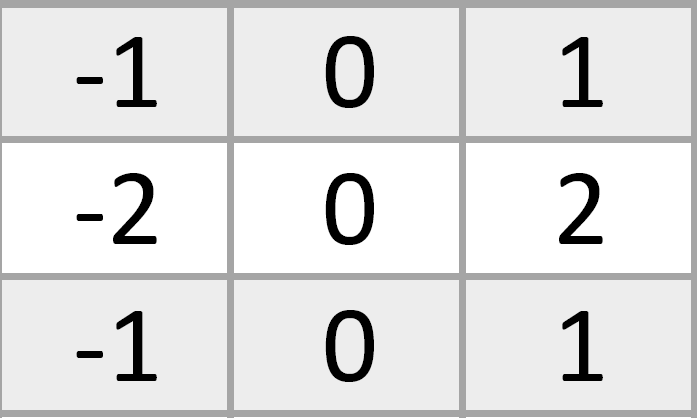
Вот такое ядро свёртки, например, сможет находить вертикальные края объекта. Если понадобится найти горизонтальные или диагональные линии краёв — повернем таблицу с множителями, чтобы нули оказались расставлены горизонтально или по диагонали. Сейчас таблица, по сути, вычитает значения пикселей слева из значений пикселей справа, игнорируя те, что посередине. Если разность окажется далекой от нуля (в положительном или отрицательном направлении), значит, слева и справа оказались разные цвета: лепесток розы закончился, начался зеленый фон. Пиксель, оказавшийся между двумя цветами, можно закрасить темным цветом, а остальные — посветлее, тогда получится вот такой красивый фильтр:


Ядро свертки — очень мощный инструмент. С помощью него компьютер может находить на картинке края объектов, углы, выяснять их наклон и резкость перехода, делать много чего другого. Поиск этих деталей — базовый «кирпичик» алгоритмов компьютерного зрения, ведь разные мелкие черточки можно рассматривать как уникальные особенности тех или иных объектов или текстур на картинке. О том, как поиск углов на изображении связан с машинным обучением, — читайте в нашей следующей статье.
А еще рекомендуем посмотреть источники, которые очень помогали при написании:


