«Системный Блокъ» уже не раз писал о сетевом анализе взаимосвязей между людьми, литературными героями и другими объектами реального и вымышленного мира. Как же определить, кто главный в этих сетях? Существует достаточно много способов сделать это с опорой на подсчеты и анализ структуры сети. Сейчас мы расскажем про пять основных мер центральности узла. Для наглядности все центральности будут продемонстрированы на сетях персонажей русских пьес.
На всякий случай маленькое напоминание: сеть (граф) — это такая модель любых объектов, имеющих связи друг с другом. Например, можно построить граф дружбы, можно — граф международной торговли или перелетов между аэропортами, а можно — граф взаимодействия вымышленных персонажей в пьесе. Главное, чтобы были сами объекты, их в сетевом анализе называют вершинами или узлами, и связи между ними — их называют ребра или дуги. Ниже представлена сеть пьесы «Скупой рыцарь» А.С. Пушкина.
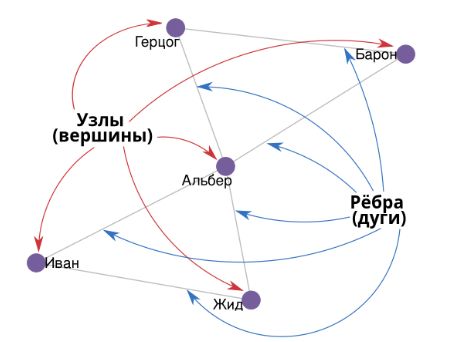
Взаимодействием в сетях пьес мы считаем появление двух персонажей в одной сцене. При этом для учета взаимодействия каждый персонаж должен произнести хотя бы одну реплику. Рёбра в графах взаимодействий между персонажами не имеют направления, так как взаимодействие между двумя персонажами считается обоюдным.
Степень (Degree)
Степень вершины показывает количество связей у вершины. Например, в сети на основе литературного произведения степень узла покажет, со сколькими персонажами взаимодействует герой на протяжении всего действия. На этой визуализации социальной сети пьесы «Горе от ума» красным цветом подписаны персонажи, имеющие степень 2 или 3 (т.е. успевшие по ходу пьесы пообщаться лишь с двумя или тремя другими героями). Видно, что это в основном слуги.
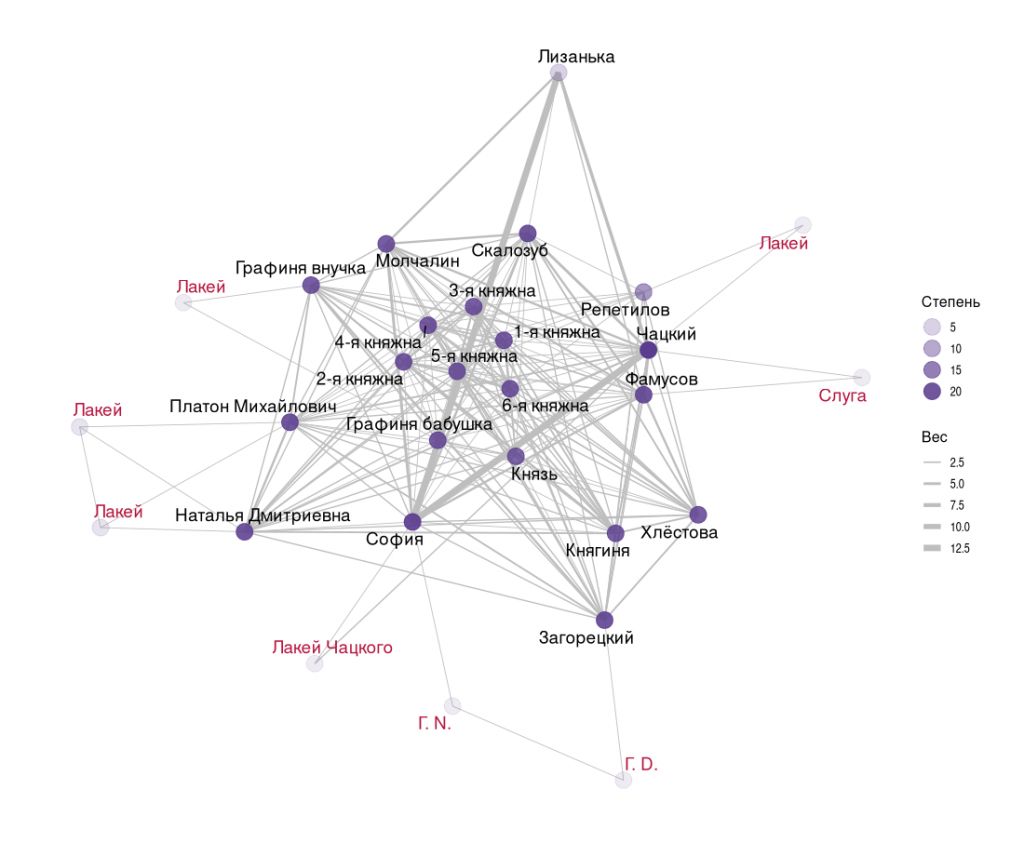
Взвешенная степень (Weighted degree, strength)
Взвешенная степень — это расширенная версия обычной степени. Она учитывает не только количество соседних вершин, но также веса рёбер. Вес может быть любым числом и показывать, например, время от одного населённого пункта до другого или сумму денег, взятую в долг (но тогда ребро должно быть направленным, чтобы показать кто кому должен).
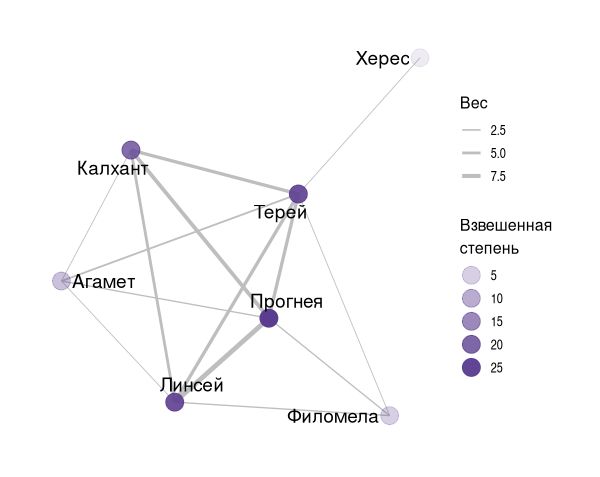
В соцсетях пьес веса связей показывают сколько раз персонажи общаются друг с другом в течение всего произведения. Другими словами, взвешенная степень учитывает количество взаимодействий между двумя персонажами. На картинке выше веса ребер отображены через толщину: видно, например, что Чацкий очень много говорит с Софьей, а сама Софья — со своей служанкой Лизанькой. Взвешенная степень каждого персонажа равна сумме всех его взаимодействий с другими действующими лицами.
Эта метрика позволяет легко определить персонажа, который больше всего взаимодействует с другими персонажами, а не только имеет больше знакомств, в отличие от обычной степени. Например, в пьесе И.А. Крылова «Филомела», Прогнея — персонаж с наибольшей взвешенной степенью, но на самом деле Терей больше связан с остальными действующими лицами и по другим метрикам он также лидирует. Подробнее о выявлении главных персонажей мы расскажем в следующем посте.
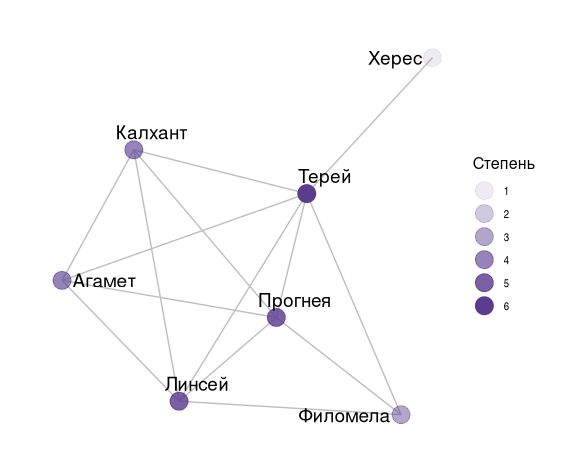
Степень близости (Closeness centrality)
Эта характеристика показывает, насколько легко попасть из данной вершины в другие узлы сети . Общая формула выглядит как
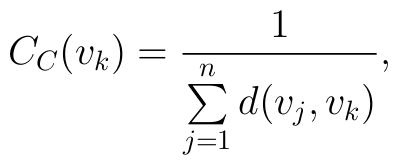
где 
— длина минимального пути между v_j и v_k.
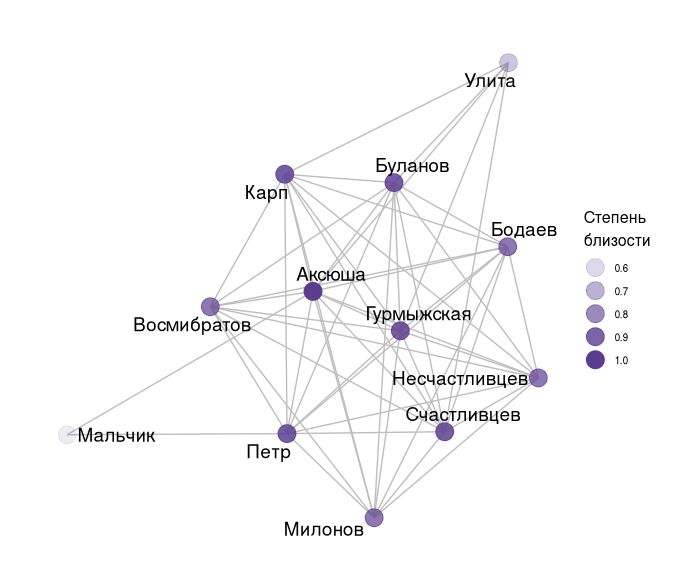
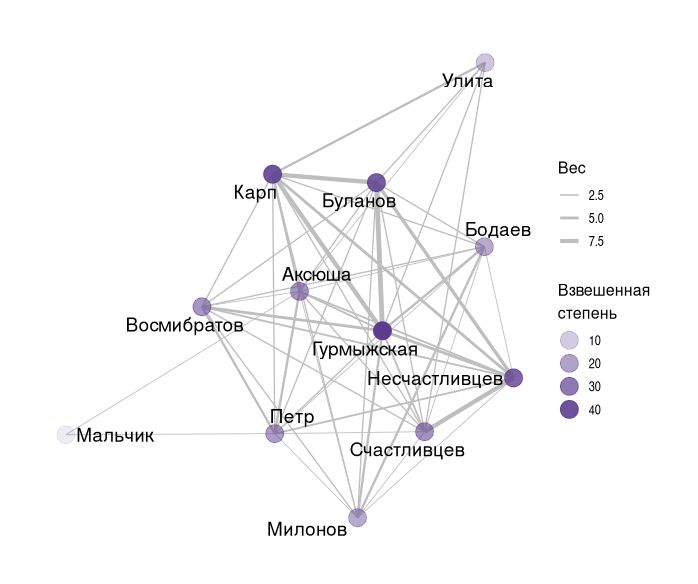
В пьесах эта метрика может означать, напрямую ли взаимодействуют с этим персонажем или нет. Например, в пьесе А. Н. Островского «Лес» персонаж Аксюша имеет невысокую взвешенную степень, но наибольшую степень близости. По сюжету, она находится в зависимом положении, в первую очередь от Гурмыжской (которая имеет наибольшую взвешенную степень), и это может означать что остальные персонажи взаимодействуют с ней напрямую, так как могут себе это позволить.
Степень посредничества (Betweenness centrality)
Степень посредничества показывает, насколько связующим является узел, и определяется как сумма вероятностей встретить данную вершину в кратчайшем пути между двумя другими. Формула выглядит следующим образом:
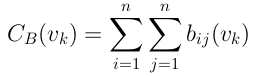
где 
— это вероятность наличия вершины vkв кратчайшем пути между вершинами 
и 
.
В терминах пьесы можно сказать, что она показывает вероятность того, что два персонажа связаны через этого персонажа. Эта характеристика помогает выявлять персонажей, которые являются посредниками при передаче информации от одной группы лиц к другой.
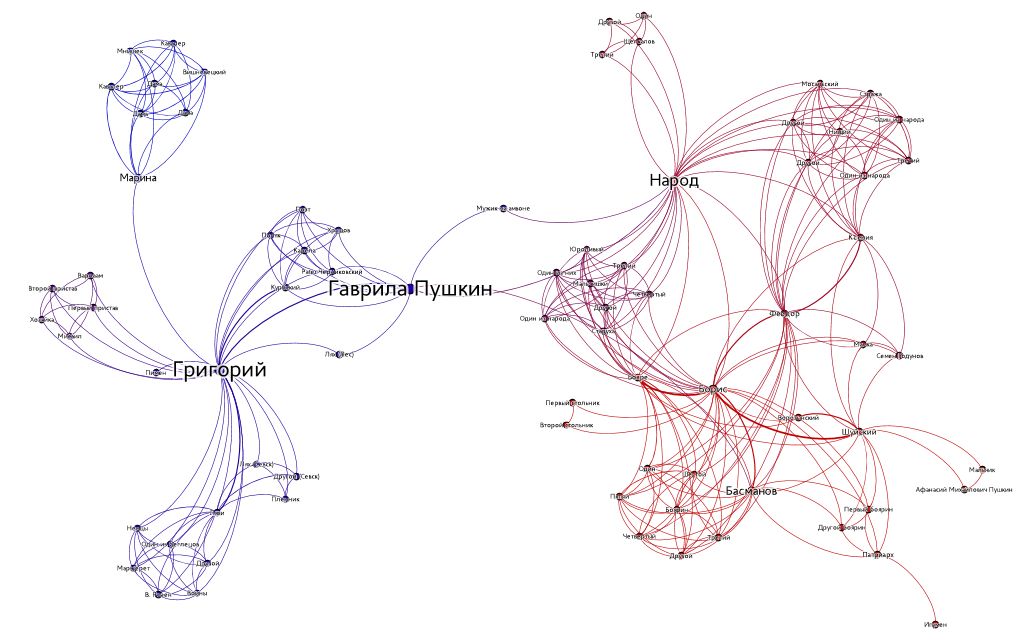
Хороший пример персонажа с высокой степенью посредничества в корпусе русской драмы — второстепенный персонаж Гаврила Пушкин из пьесы «Борис Годунов» А.С. Пушкина. Наибольшая степень посредничества в этой сети у самозванца Григория Отрепьева (который к концу действия превращается в «Димитрия I», будущего Лжедмитрия I), но сразу за ним идёт сравнительно малозаметный по ходу пьеса Гаврила Пушкин. По сюжету, он является связующим персонажем между приближёнными Бориса и Григорием. При прочтении легко не заметить важность этого персонажа, однако на визуализации сети пьесы хорошо видно, что Гаврила связывает два кластера — персонажей в Москве и в Польше. И действительно: он ездит между странами со своего рода дипломатическими миссиями, когда будущий Лжедмитрий и царь Борис еще пытаются решить дело миром, затем он же подговаривает лучшего воеводу Годунова — Басманова — перейти на сторону самозванца; в конце пьесы именно Гаврила Пушкин идет зачитывать первые указы нового царя народу (который в пьесе является вполне самостоятельным персонажем, имеет свои реплики и образует третий большой кластер).
Степень влиятельности (Eigenvector centrality)
Степень влиятельности показывает важность персонажа, учитывая влиятельность персонажей, с которыми взаимодействует данный персонаж. В пьесах эта метрика позволяет разделить действующих лиц на «центральных» и «периферийных». Персонажи более значимы, если они взаимодействуют с персонажами важнее себя, и теряют свою значимость при контакте с менее важными действующими лицами.
Эта метрика определяется немного сложнее, чем предыдущие, но если вас не пугает щепотка линейной алгебры, то следующие несколько абзацев для вас.
Для начала стоит рассказать о способе представления сети в виде матрицы. Такая матрица называется матрицей смежности, так как её элементы показывают, смежны ли вершины друг с другом. Например, составим матрицу смежности для уже сети уже упоминавшейся пьесы «Скупой рыцарь».
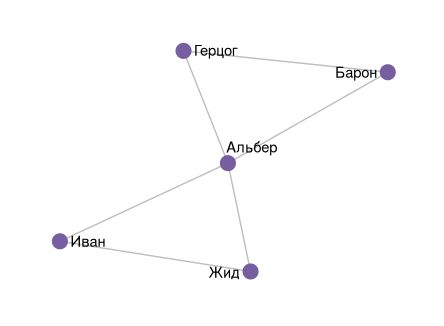
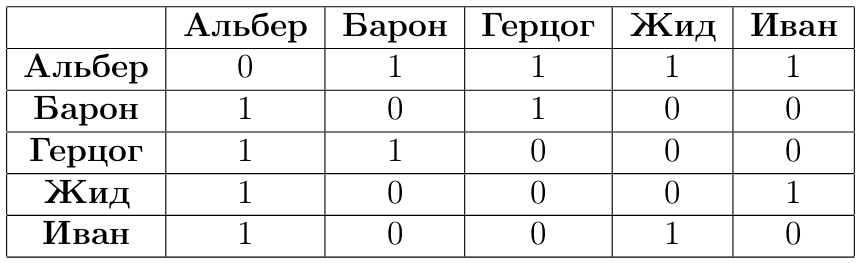
Итоговую матрицу обозначим А:
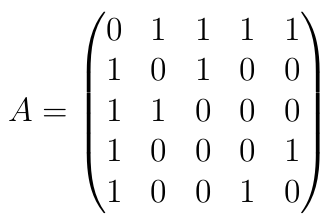
Единицами отмечено наличие рёбер между персонажами, а нулями соответственно их отсутствие. Вместо единиц в матрице могут быть указаны веса рёбер и тогда уже матрица будет взвешенной. Заметим, что получившаяся матрица является симметричной.
У таких матриц есть важное свойство — наличие собственных векторов. Это такие вектора, произведение которых на матрицу эквивалентно произведению числа на этот вектор. Формально это записывается вот так:
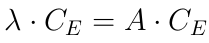
где А — это матрица смежности;
λ — действительное число;
С_E — собственный вектор матрицы А.
Элементы вектор C_E и являются степенями влиятельности для каждой вершины. Если определить вектор С_E как 
, то предыдущее равенство можно переписать в линейном виде для отдельной вершины:
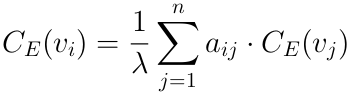
где С_E(v_i) — это степень влиятельности вершины v_i;
a_ij — элемент матрицы A, расположенный в i-й строке и j-м столбце.
В такой записи лучше видно, что на степень влиятельности вершины v_i влияют значения всех остальных вершин.
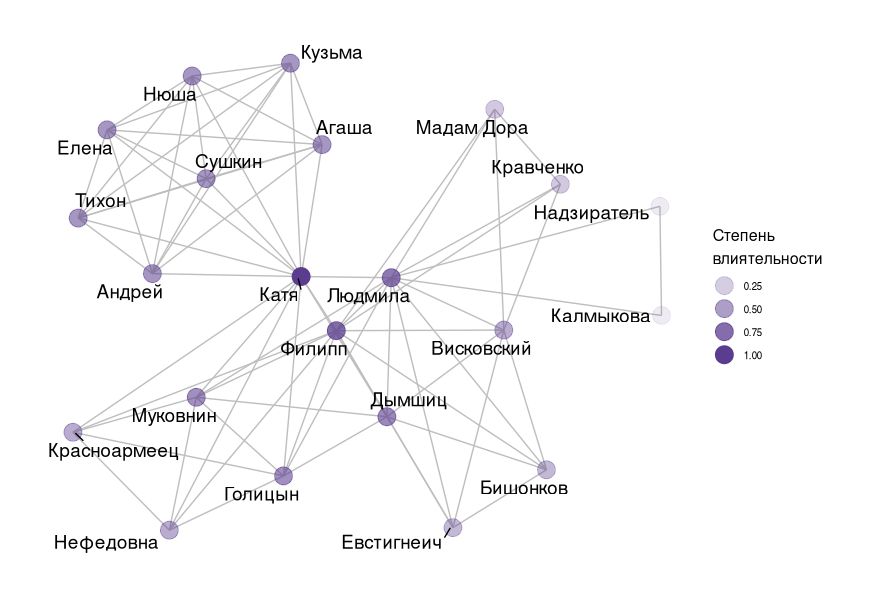
В пьесе «Мария» И.Е. Бабеля Катя имеет наибольшее значение степени влиятельности, и все персонажи, которые связаны с ней, имеют большие показатели, чем те кто не взаимодействует с Катей на прямую. Также интересна группа персонажей, которая взаимодействует только с Катей (Агаша, Кузьма, Нюша и др.) и соответственно они имеют более высокую степень влиятельности, чем большинство персонажей из другой части графа.
Заключение
Кроме перечисленных мер центральности существует ещё много других полезных и более сложных характеристик, таких как PageRank (ее когда-то придумали основатели Google для ранжирования страниц в интернете), центральность узла по Кацу и другие. Тем не менее пять описанных нами метрик являются основными для сетевого анализа. В следующей статье мы расскажем, как с их помощью можно исследовать структурные особенности шедевров русской драматургии и получить новый взгляд на систему персонажей классических пьес.
