KNN — это модель машинного обучения, которая основана на следующей идее: если объекты похожи по одним характеристикам, то будут похожи и по другим. Например, если две квартиры расположены в одном районе, построены в одно и то же время и имеют схожую по размеру жилплощадь, то с большой вероятностью их стоимость будет почти одинаковой.
KNN часто применяется в системах рекомендаций: для пользователя находят других похожих на него пользователей и рекомендуют ему те же товары, фильмы или услуги. Также этот метод используется в некоторых экономических задачах и в медицине.
Для чего нужен KNN
Метод KNN (K Nearest Neighbours — K ближайших соседей) решает задачи классификации и регрессии. Пример задачи классификации: определить породу собаки по набору её характеристик. Пример задачи регрессии: по описанию квартиры предсказать её стоимость.
В обеих задачах выделяют объект — по чему делается предсказание (собака или квартира) и целевую переменную — то, что надо предсказать (порода, цена на квартиру). Подробнее о задачах классификации и регрессии можно прочитать в нашем материале о машинном обучении.
Скажи, кто твой сосед, и я скажу, кто ты
Согласно данному методу, если объекты «похожи», то их целевые переменные принимают те же (в случае классификации) или близкие (в случае регресии) значения. Однако в отличие от людей компьютер не может просто сравнить две квартиры или двух собак. Он понимает лишь числа, поэтому и объекты нужно описывать числами.
К примеру, квартиру можно описать величиной жилой площади, количеством комнат, расстоянием до метро; собаку — длиной её конечностей. То есть сопоставляется набор характеристик, которые выражаются через числа. Такие наборы компьютер может сравнить довольно легко — достаточно лишь подсчитать разности, возведённые в квадрат между соответствующими значениями для каждой характеристики, и сложить их. Квадратный корень полученной суммы называют расстоянием между двумя объектами.
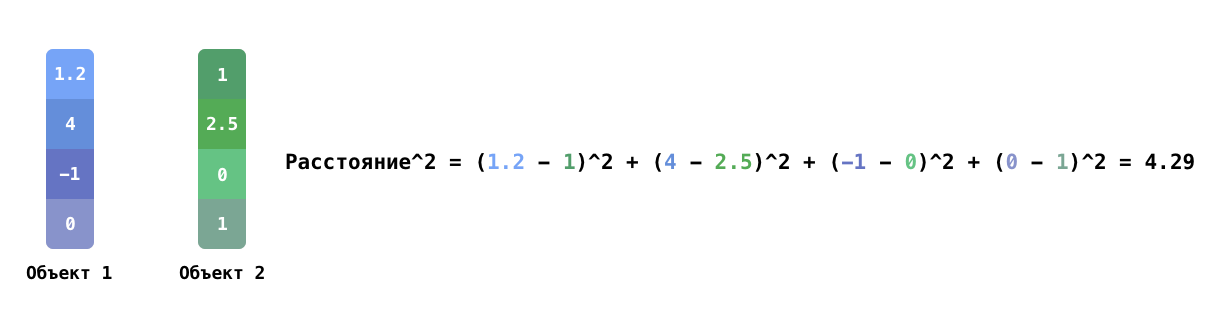
Пример подсчёта квадрата расстояния между двумя объектами с четырьмя характеристиками
Расстояние можно считать и по-разному: например, вместо квадратов разности использовать модуль разности. Выбор способа подсчёта расстояния между объектами влияет на свойства и качество модели и зависит от задачи.
Предсказание целевой переменной для данного объекта делается на основе нескольких объектов, похожих на него. Такие объекты называют «соседями». Для этого вычисляются расстояния между объектом и всеми объектами обучающей выборки, а затем по подсчитанным расстояниям отбираются K ближайших соседей.
Число K чаще всего не слишком маленькое, поскольку иначе есть риск найти нерепрезентативного соседа. Например, если при K = 1 в обучающей выборке нашлась квартира, похожая на данную, но в объявлении указана неправильная цена, предсказание тоже будет ошибочным.
K не должно быть слишком большим, потому что на предсказание не должны влиять слишком непохожие соседи. Точное значение K определяется перебором разных значений и замером качества предсказаний на валидационной выборке при каждом тестируемом значении.
Как делается предсказание: голосование и усреднение
После того, как K соседей найдены, предсказание целевой переменной будет вычисляться по-разному в зависимости от задачи. В случае классификации в качестве предсказания берётся самый популярный класс среди соседей. Например, если в задаче предсказания породы собаки среди соседей присутствуют 5 хаски и 2 маламута (K в этом случае равно 7), то предсказанием будет порода хаски. В некоторых случаях у соседей не всегда равное количество голосов. Вес голоса иногда определяется близостью соседа или заранее задан для каждого класса.
В случае задачи регрессии значения целевых переменных соседей усредняются. Конкретный способ усреднения зависит от задачи: в некоторых задачах достаточно обычного среднего арифметического, в других соседям присваивают вес, который зависит от близости соседа, а затем считают взвешенное среднее. Также довольно часто используют медиану.
Когда метод KNN сложно применять
Как говорилось ранее, соседи для данного объекта ищутся в обучающей выборке. Однако бывают случаи, когда найти информативных соседей становится трудно. Такое часто происходит, если объекты описываются большим количеством характеристик — и чем больше их число, тем меньше будет похожих соседей.
Для того, чтобы это нивелировать, необходимо экспоненциально увеличивать размер обучающей выборки. Например, если для объектов с четырьмя характеристиками необходима обучающая выборка размера N, то при добавлении четырёх новых характеристик (итого восемь) потребуется обучающая выборка размера N в квадрате. Такая проблема называется «Проклятием размерности».
Другое ограничение метода исходит из необходимости поиска соседей. При наивной реализации метода для нахождения нескольких соседей необходимо считать расстояния до всех объектов обучающей выборки (что крайне ресурсозатратно, если выборка объёмная). Существуют методы приближённого поиска соседей, которые не требуют такого большого количества вычислений, однако для работы метода всё равно необходимо хранить всю обучающую выборку.
Источники
1. Evelyn F., Joseph H. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties // Journal of the American Statistical Association. 1953. №264. Pp. 850–898.
2. Thomas C., Peter H. Nearest neighbor pattern classification // IEEE Transactions on Information Theory. 1967. №13(1). Pp 21–27.


