Нейросети сейчас везде, и даже цифровому гуманитарию от них не скрыться. Word2vec при помощи нейросети кодирует смысл слов (вот тут мы объясняли, как), а новые модели ELMO и BERT даже научились учитывать, что слова появляются в разных контекстах и от этого из смысл тоже может меняться. Этот текст — про то, что значит «обучить» нейросеть и кто «подбирает веса» отдельных нейронов.
А что вообще творится в нейросетях? Напомните!
Ранее мы рассказывали, как «сырые» данные (картинка, видео или текст) разбиваются на мелкие кусочки и подаются на каждый входной нейрон. Дальше входные нейроны анализируют что-то очень простое — есть ли в их кусочке картинки 10 белых пикселей, есть ли буква «Т» в слове — и если да, нейрон «активируется», то есть передает свой сигнал в следующий слой с определенной силой. Сигналы комбинируются, потом собираются в абстрактные комбинации десятков комбинаций сигналов, и в конце концов активируют один из нейронов, который классифицирует картинку как котика или хлеб.
А как активируется нейрон?
Нейрон — это функция, которая получает на вход числа (обычно много), что-то с ними делает и возвращает одно число (обычно от 0 до 1). Функция, из которой нейрон состоит, называется функцией активации, или передаточной функцией. Именно она отвечает за то, будет ли передан сигнал нейрона дальше (1 на выходе функции — если будет, 0 — если нет). В самом простом виде функция активации может быть пороговой:
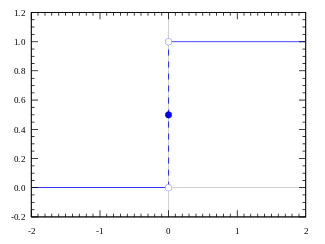
В данном случае, если какие-то значения на входе нейрона дали положительную сумму — нейрон активировался. Порог активации здесь выглядит как вертикальная палочка, простой переключатель вкл/выкл, а значит, нейрон может быть либо активен, либо нет — как лампочка. Есть и более сложные функции, которые могут изменять силу выходного сигнала, могут «чуть-чуть активировать» нейрон, или «активировать его посильнее»:
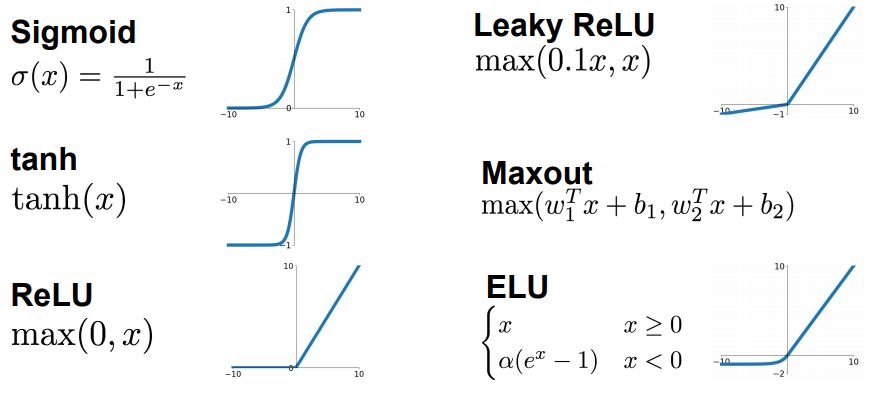
Выбор функции активации нейронов влияет на то, какие задачи они могут решать, и их подбор — задача создателя нейросети. Если создатель понимает, какие функции для чего подходят, у него больше шансов сделать крутую нейросеть, которая решит его проблему.
Вот главное: нейрон — это функция. Чем больше ее значение, тем важнее сигнал нейрона для всей сети.
Почему это важно в контексте обучения нейросети?
Коротко: нейроны постоянно дают слишком сильный или слабый сигнал и сбивают предсказание, их нужно настраивать.
Нейроны глупые! Без ручной настройки силы их выходных сигналов нейросеть даёт случайные предсказания. К выходному значению нейрона можно (и нужно) прибавлять некоторый вес. Вес прибавляется или отнимается в зависимости от того, насколько сильно в прошлый раз нейросеть ошиблась с предсказанием. Этот этап работы, когда нейроны штрафуются за все прошлые «косяки», называется обратным распространением ошибки. Какие-то нейроны активируются слишком сильно, какие-то — слабо, но все равно они уводят предсказание нейросети в сторону от правильного. Поскольку нейронов слишком много, и за какие конкретно признаки каждый из них отвечает — неясно, настроить каждый вес вручную невозможно. Люди придумали способ настраивать веса автоматически.
Для этого существует функция потерь. Что она делает?
Коротко: ее значение возрастает, если нейросеть сильно ошибается. Значит, надо найти такое решение, где функция возрастать не будет.
Есть функция, возрастающая при сильной ошибке предсказания. Чем больше ошибка, тем сильнее уменьшаются (штрафуются) веса активированных нейронов. Человеку нужно свести меру ошибки к минимуму, научить нейросеть делать верные предсказания о том, котик на картинке или булочка. Если функция потерь дает высокие значения при большой ошибке, мы просто ищем такие веса, при которых она дает минимальные значения.
Кстати, функций потерь тоже существует много, они по-разному подходят для разных задач, и крутые программисты за 300к/сек знают, как в них сориентироваться. Функции потерь объединяет то, что они возрастают вместе с мерой ошибки предсказания. Она вычисляется просто: из числа X (предсказанного) вычитаем число Y (то, что должно было предсказаться) — получаем число Err. Оно становится одним из аргументов функции потерь.
Здесь надо вспомнить производные
Задача подбора весов нейронной сети также называется тренировкой или задачей оптимизации. (Ведь optimus — наилучший, а значит, мы и ищем лучшие веса?) Веса нам нужны те, при которых функция потерь принимает минимальное значение. Когда мы знаем это значение, рассчитать нужные веса становится легко — все равно, что решить уравнение.
А значит, желаемая схема обучения нейросети выглядит примерно так:
Функция потерь принимает минимальное значение → находим соответствующие этому значению веса → ошибка минимальна → предсказание нейросети точно → вы великолепны.
Только сначала нужно найти минимальное значение функции.
Как это делали в школе?
Когда на уроке алгебры учительница давала какой-нибудь многочлен и просила найти его минимум, мы поступали следующим образом:
- Находили производную функции и приравнивали ее к нулю;
- Решали получившееся уравнение, то есть находили, при каких значениях переменной производная равна нулю;
- Подставляли эти значения в функцию и проверяли, где получится минимальное значение.
Напомним, что производная функции выражает скорость ее возрастания или убывания. Её геометрический смысл — показать угол, под которым в данной точке проходит касательная к функции. Если производную (а значит, угол касательной) приравнять к нулю, то мы найдем точки, в которых касательная параллельна оси абсцисс.
Вот что это будут за точки: в них функция меняет направление. Такие точки обязательно становятся (хотя бы локальными) минимумами или максимумами функции. А вот как будут выглядеть касательные к этим точкам:
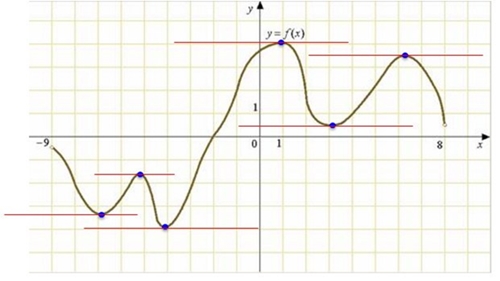
После этого (страшного или приятного?) математического флешбэка пора признаваться, что как раз вот так в нейронных сетях найти минимум функции потерь невозможно. У нее слишком много входных аргументов, и аналитические подходы (как показанный выше) не работают. Приходится применять специальный поисковой, пошаговый метод градиентного спуска (умное слово для него — «эвристический», то есть все тот же «поисковой», но еще умнее — по-гречески).
Вот главное: нам до сих пор нужно найти минимальное значение функции потерь, это минимизирует ошибку в предсказании нейросети. Но мы сейчас выяснили, что по-школьному это сделать не получится.
We need to go deeper
Если есть функция, зависящая от нескольких переменных, можно говорить о частной производной, то есть о такой производной, когда все остальные переменные, кроме той, которая нам интересна, становятся константами (то есть постоянными).

Поэтому вот вам таблица, попробуйте сказать, чему равна частная производная от переменной x функции
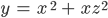
Помните, что если рассчитывать производную от x, то z становится константой и с ней ничего делать не нужно.
(Ответ будет чуть ниже, не подглядывайте!)
Математически фразу «производная функции y от переменной x» можно записать так:
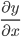
Ответ к задаче: частная производная равна
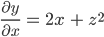
Чему же равна частная производная в точке (x=3, z=4)? Теперь мы можем просто подставить значения 3 и 4 в полученное уравнение частной производной
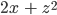
Мы получим, что производная равна 23 + 44 = 22.
Пора рассказать, что такое градиент
Если для функции многих переменных по очереди рассчитать частные производные для каждой из переменных (и записать эти производные в ряд, и взять в скобочки), получится вектор, называемый градиентом. Так как одна переменная соответствует одной координатной оси, каждый элемент вектора показывает скорость изменения функции вдоль своей оси, а все вместе они показывают направление, в котором быстрее всего возрастает функция в целом.
Вот главное: градиент — это вектор, показывающий направление, в котором функция многих переменных быстрее всего возрастает или падает. «Градиент функции f» записывается так: ∇f (можно читать как «набла f»).
Вот небольшое упражнение. Попробуйте найти градиент функции
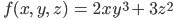
для переменных x, y, z?
Подсказка: должен получиться вектор с тремя элементами.
Ответ:
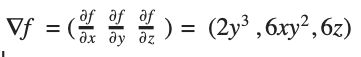
Сложность в том, чтобы уследить, какие из «констант» — множители переменной, что рассматриваются в данный момент, а какие — отбрасываются как слагаемые.
Объясните наконец, что такое градиентный спуск!
Градиентный спуск — это эвристический алгоритм, который выбирает случайную точку, рассчитывает направление скорейшего убывания функции (пользуясь градиентом функции в данной точке), а затем пошагово рассчитывает новые значения функции, двигаясь в выбранную сторону. Если убывание значения функции становится слишком медленным, алгоритм останавливается и говорит, что нашел минимум.
Стоит помнить, что говорим не о двумерных функциях. Представить, что происходит, можно по этой картинке:
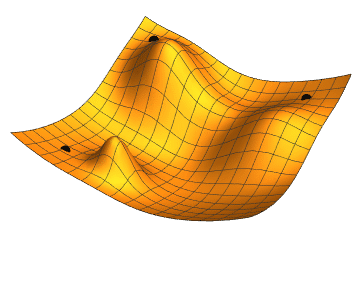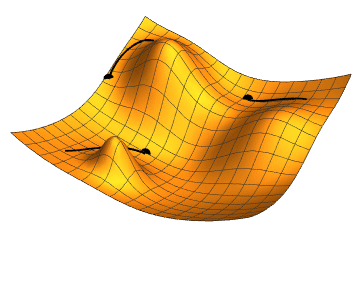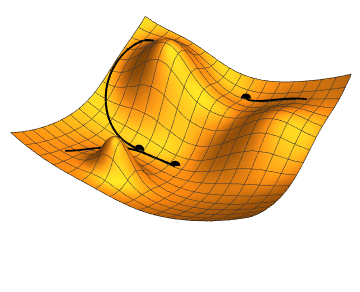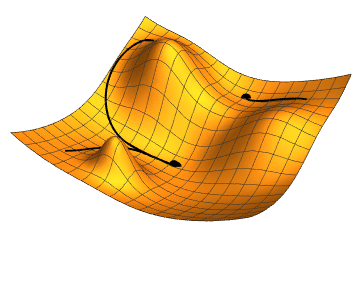
Градиентный спуск выбирает случайную точку, находит направление самого быстрого убывания функции и двигается до ближайшего минимума вдоль этого направления. Кстати, размер одного шага можно настроить, это бывает очень важно. Если на каком-то этапе разность между старой точкой (до шага) и новой снижается ниже предела, считается, что минимум найден, алгоритм завершен. Можно вообразить работу градиентного спуска как игру в «холодно-горячо» до тех пор, пока степень «потепления» не станет пренебрежительно малой.
Вот главное:
- Градиентный спуск выбирает случайную точку старая_точка, принадлежащую функции
- Новая_точка рассчитывается как старая_точка минус (размер_шага * градиент_в_старой_точке)
- ЕСЛИ модуль (новая_точка минус старая_точка) < порогового_предела
ТО старая_точка = минимум функции
ИНАЧЕ — повторить алгоритм для новая_точка
А зачем настраивать размер шага?
Коротко: чтобы не пропустить минимум.
Размер шага алгоритма определяет, насколько мы собираемся двигать точку на функции потерь, и этот параметр называется «скоростью обучения». Слегка запутывающее название, поскольку не всегда высокая скорость обучения гарантирует хороший результат. Скорее скорость обучения стоит воспринимать как ширину шагов, с которыми человек с завязанными глазами ищет, где «горячо» или «холодно». В некоторых случаях бывает так, что слишком широкие шаги вообще не позволяют достичь минимума, и машина бесконечно перешагивает через него, затем градиент «разворачивает» ее обратно, и алгоритм снова перескакивает через минимум. Маленькая скорость обучения хоть и придает точности, зато, конечно, увеличивает время на обучение нейросети.
А почему это вообще должно работать?
Градиентный спуск ищет ближайшую к случайно выбранной точке впадину на графике функции. А поскольку в нейросетях функции очень сложные и локальных впадин-минимумов на них много, такой подход должен быть неэффективен в вопросах обучения нейросети и всегда натыкаться на локальные минимумы.
Тем не менее градиентный спуск как метод обучения почему-то работает хорошо. В 2015 группа ученых из Курантовского института математических наук в Нью-Йорке нашла этому объяснение, показав, что большая часть локальных минимумов функций потерь, используемых в нейросетях, располагается близко к глобальному минимуму. Эта близость и позволяет натренированным при помощи градиентного спуска нейросетям справляться с задачами достаточно эффективно.
Надеемся, что теперь вы разобрались с тем, что значит «подобрать веса» или «обучить нейросеть», а также с тем, на что уходит такое большое количество времени и ресурсов при тренировке (спойлер: на повторяющуюся монотонную подстановку переменных в градиент функции и на пошаговую коррекцию весов нейросети после предсказания).
Источники
- Градиентный спуск: всё, что нужно знать
- Математика для искусственных нейронных сетей для новичков, часть 2 — градиентный спуск


