О чём пойдёт речь
Это первая часть нашего материала о механизмах работы больших языковых моделей. Мы объясняем понятие интерпретируемости, рассказываем о том, как работает базовый компонент всех нейросетей и почему исследователям сложно разобраться в внутреннем устройств моделей.
Во второй части мы расскажем, как метод, разработанный в компании Anthropic, позволяет выявлять, какими концепциями оперируют большие языковые модели и как с его помощью можно контролировать их «поведение».
Интерпретируемость нейронных сетей: чем плох чёрный ящик
Нейросети доказали свою эффективность в решении большого набора задач, значительно превзойдя большинство других моделей машинного обучения. Однако они почти всегда работают как «черный ящик» (black box): на вход подаются исходные данные, далее с ними происходят абстрактные математические преобразования, и в итоге выдаётся ответ. Изложить в понятных человеку категориях, как он был получен и что именно на него повлияла, такие модели в общем случае не могут.
Другими словами, нейросети позволяют хорошо моделировать зависимость между входом и выходом, но не предоставляют «объяснения» того, как именно эта зависимость устроена. Например, обычная модель для классификации изображений отлично различает породы собак, но из неё проблематично извлечь знание о том, по каким признакам можно отличить фотографию хаски от маламута.
Нейросеть — механизм, устройство которого сложно интерпретировать
Нейросеть, которая оценивает риски при выдаче кредитов, может делать это значительно точнее человека, но не «способна» дать обоснование своей оценки, а без объяснения клиент банка так и не узнает причину отказа.
Свойство модели, позволяющее наблюдателю объяснить внутреннее устройство и механизм её работы, называется интерпретируемостью. Плохая интерпретируемость нейросетей тормозит, например, их применение в медицине или в сфере управления сложными системами, сбои которых могут приводить к большим убыткам.
Лучшее понимание внутреннего устройства моделей могло бы позволить исследователям их улучшать и лучше контролировать. Например, даже передовые языковые модели могут галлюцинировать, то есть генерировать ложную информацию. Обычно это происходит, когда информации о задаваемом вопросе не было в обучающей выборке. Проблема состоит в том, что задача определения границ «знаний» языковых моделей до сих пор не решена. Если бы существовал способ отслеживания всей цепочки вывода ответа, отслеживание галлюцинаций было бы возможно.
Другая причина, по которой исследователи хотят добиться высокой интерпретируемости, — это вытекающая из неё способность контроля над моделью. Так, понимая устройство языковой модели, можно, например, «удалить» из неё нежелательную информацию вроде рецептов опасных веществ или убрать возможность генерировать вредоносный код.
Перцептрон: цифровой двойник нейрона
Вспомним, как устроен базовый блок практически любой нейронной сети — перцептрон. Перцептрон — это математическая модель биологического нейрона. Биологический нейрон устроен сложнее этой модели, но в главном они похожи: нервная клетка имеет несколько точек входа сигнала (дендриты), имеет выходной канал (аксон) и может возбуждаться в ответ на входящий сигнал. В литературе про машинное обучение понятия «перцептрон» и «нейрон» (уже не биологический, искусственная модель) часто взаимозаменяемы.
Зачем уметь моделировать на компьютере возбуждаемую нервную клетку? Для ответа на этот вопрос рассмотрим задачу классификации изображений c левым («/») и правым («\») слешами:
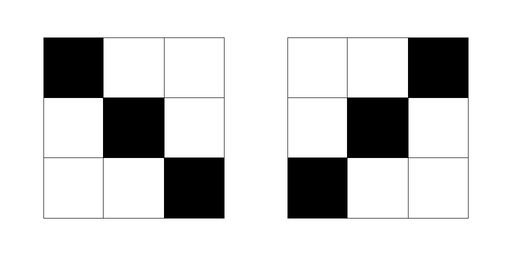
Изображения с левым и правым слешами. Каждая клетка — пиксель, размер изображений — 3×3 пикселей
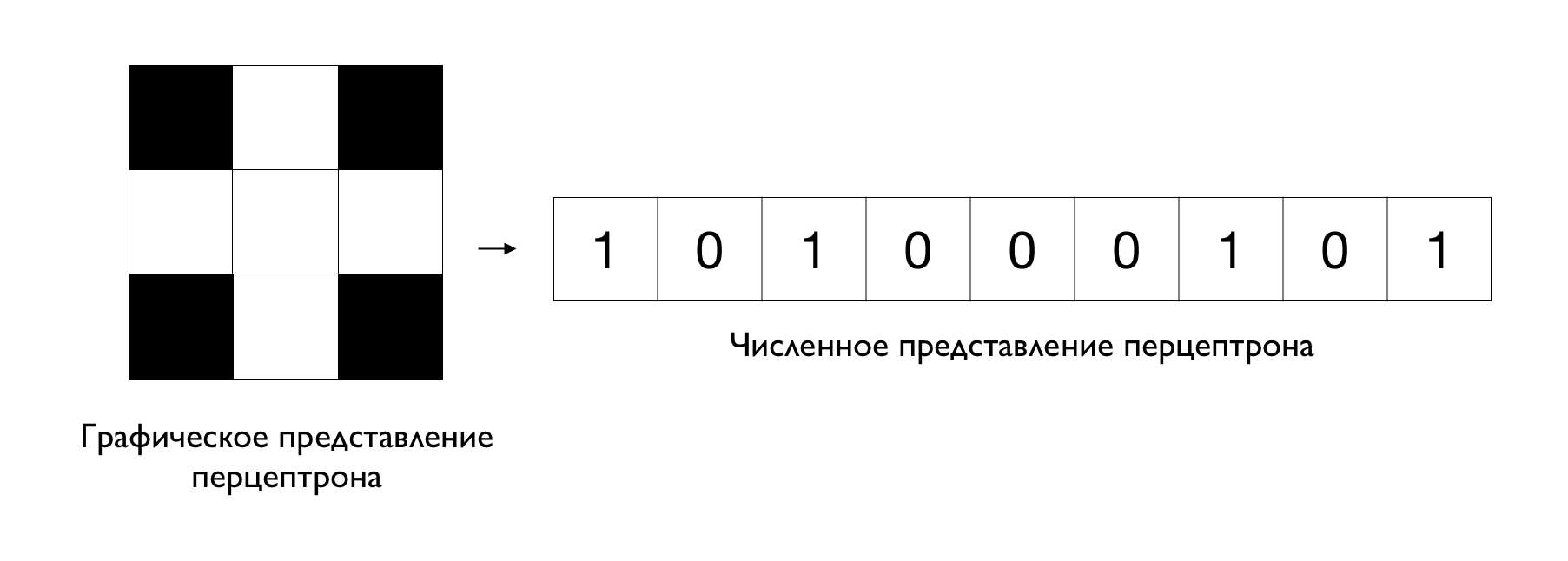
Изображение можно представить в виде таблицы чисел, которая будет «понятна» компьютеру. В таблице каждую чёрный клетку обозначим 1, а белую — 0:
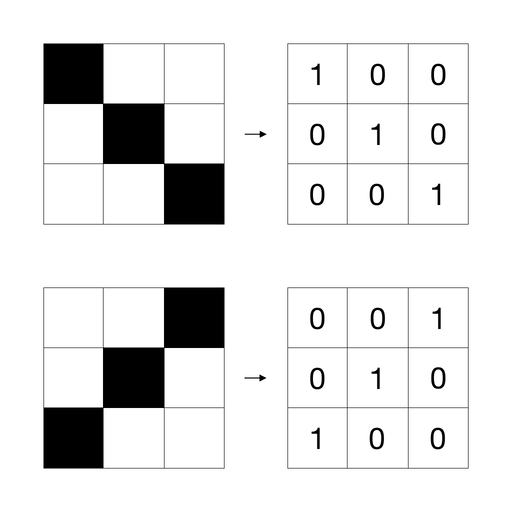
Представление изображений в виде таблицы с числами
Далее для каждой таблицы все строки расположим в один ряд:
- для «\»: 1, 0, 0, 0, 1, 0, 0, 0, 1;
- для «/»: 0, 0, 1, 0, 1, 0, 1, 0, 0.
Эти два набора чисел являются представлениями исходных изображений, с которыми удобно работать компьютеру. Для решения задачи будет использоваться перцептрон. Перцептрон представляется также набором чисел, которые подбираются в процессе его обучения. Степень возбуждения перцептрона — она же активация, — выражается числом, которое равно сумме произведений соответствующих чисел входных данных и перцептрона. Рассмотрим пример расчёта активации перцептрона, когда вход описывается тремя числами (тогда и перцептрон задаётся тремя числами):

i1, i2, i3 — числа, задающие входные данные, w1, w2, w3 задают перцептрон
Аналогично рассчитывается значение активации при любом размере входа. Чем больше значение активации, тем больше возбудился перцептрон, и наоборот.
Строго говоря, общепринятое определение отличается от данного выше: к значению активации применяется нелинейная функция (функция, графиком которой не является прямая линия). Например, функция ReLU возвращает ноль, если значение активации меньше 0, и исходное значение в остальных случаях. Другими словами, происходит фильтрация, при которой все негативные активации равнозначны, а позитивные — нет.
Это отличие в определении не так важно в контексте этой статьи, поэтому для простоты мы не будем его учитывать.
Простейшая нейросеть — это набор нескольких разных перцептронов. В таком случае выходом будет не одна активация, а набор активаций всех перцептронов.
Чтобы решить задачу классификации изображений с разными слешами, можно подобрать следующие два перцептрона:
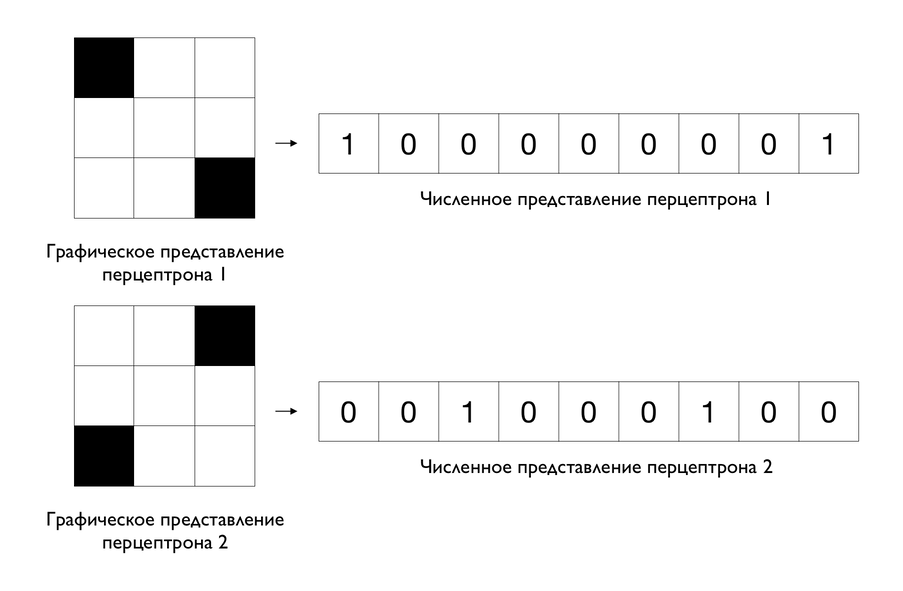
В нашем примере численное представление перцептрона можно представить как изображение, применив процедуру конвертации изображения в набор чисел, описанную выше, в обратном порядке
Посчитаем их активацию с представлениями изображений «\» и «/»:
- Для «\»:
активация перцептрона 1 равна (1, 0, 0, 0, 1, 0, 0, 0, 1) * (1, 0, 0, 0, 0, 0, 0, 0, 1) = 2;
активация перцептрона 2 равна (1, 0, 0, 0, 1, 0, 0, 0, 1) * (0, 0, 1, 0, 0, 0, 1, 0, 0) = 0;
выход: (2, 0).
- Для «/»:
активация перцептрона 1 равна (0, 0, 1, 0, 1, 0, 1, 0, 0) * (1, 0, 0, 0, 0, 0, 0, 0, 1) = 0;
активация перцептрона 2 равна (0, 0, 1, 0, 1, 0, 1, 0, 0) * (0, 0, 1, 0, 0, 0, 1, 0, 0) = 2;
выход: (0, 2).
Таким образом, перцептрон 1 возбуждается на изображение «\» и не возбуждается на изображение «/», а перцептрон 2 работает ровно наоборот. Чтобы получить ответ на задачу, нужно просто сравнить первую активацию со второй: если первая больше, значит, на изображении «\», иначе — «/».
Можно заметить, что графические представления перцептронов соответствуют признакам входных изображений, по которым их можно различить. Первый перцептрон соответствует концам левого слэша «\», а второй — концам правого «/». Совпадение тех или иных концов и является признаком для классификации. В этом и заключается функция перцептрона — распознавать в данных признаки, которые необходимы для решения задачи.
Рассмотрим в качестве примера более сложную нейронную сеть — Word2Vec. По сути эта модель — большая таблица чисел, в которой каждая строка является векторным представлением (оно же embedding) слова в корпусе. Количество строк равно количеству слов в словаре, который был сформирован до обучения модели, а количество столбцов равно количеству перцептронов:
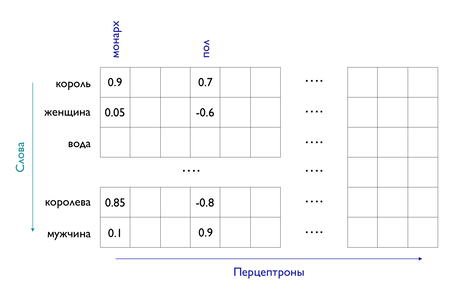
Иллюстрация работы Word2Vec
Каждый столбец соответствует одному перцептрону, который в свою очередь отвечает за определённый признак или набор признаков слов. Это может быть, например, наличие королевского титула или пол. В реальной жизни признаки могут быть не настолько простыми и понятными человеку.
В предыдущем примере каждый перцептрон применялся к численному представлению изображения. К чему применяются перцептроны Word2Vec? К численным представлениям слов, как в мешке слов. Каждому слову с номером n в словаре соответствует набор чисел, где на n-й позиции стоит единица, а на всех остальных — нули. Например, если всего в словаре 5 слов, то третье слово в нём будет представлено набором (0, 0, 1, 0, 0).
Заметим, что если применять каждый перцептрон к таким представлениям слов, то активация перцептрона равна его n-му значению, потому что все остальные значения умножаются на ноль. Таким образом, набором всех активаций для n-го слова будет являться n-я строка в таблице. Иначе говоря, векторное представление слова — это набор активаций всех перцептронов для него.
Моносемантичность и полисемантичность: как много берёт на себя перцептрон
Важно отметить, что в примере с классификацией изображений «/» и «\» в активациях для каждого изображения только одно ненулевое значение. Это означает, что каждый перцептрон активируется только на одном признаке. Однако в сложных нейронных сетях почти всегда большинство перцептронов активируется одновременно на нескольких признаках. Например, рассмотрим такой нейрон:
Перцептрон, который активируется сразу на два признака
На обоих изображениях этот перцептрон активируется с одинаковой силой, потому что он отвечает одновременно за признаки правого и левого слеша.
Перцептрон, который соответствуют сразу нескольким признакам, называется полисемантичным, а перцептрон, соответствующий одному признаку, — моносемантичным.
Полисемантичность возникает практически всегда независимо от типа данных и типа нейросети. Например, один перцептрон в Word2Vec может активироваться на разные семантические характеристики слова, а перцептрон в классификаторах изображений может отвечать за определение границ объекта и распознавание его наклона.
Как понять, за что отвечает перцептрон?
Именно полисемантичные перцептроны «виноваты» в плохой интерпретируемости нейросетей. Для того, чтобы разобраться, почему это так, рассмотрим процедуру, с помощью которой исследователи пытаются понять устройство нейросети.
- Для начала берут определённый слой нейросети: как правило, средний, поскольку первые слои ответственны за простые и абстрактные признаки, а последние — за специализированные.
- Затем на вход модели подают набор тестовых данных. Результат этого шага — набор активаций перцептронов выбранного слоя.
- После выбирается конкретный перцептрон. Для его исследования нужно из всех активаций взять только активации, соответствующие ему.
- Далее необходимо определить, на каких входных данных активации высокие, а на каких — низкие. Другими словами, определить, на каких данных перцептрон активируется, а на каких — нет. Исходя из полученных групп, можно предположить, за какой признак отвечает перцептрон.
Давайте применим эту процедуру к Word2Vec:
- Word2Vec состоит из одного слоя, в котором N перцептронов, N может варьироваться от нескольких десятков до тысяч. Как было объяснено выше, выходом этой модели является векторное представление слова, которое на самом деле является набором активаций всех перцептронов.
- Допустим, мы подали на вход модели слова: «кролик», «слон», «кровать», «стол», «бежать», «прыгнуть». Модель нам вернёт шесть наборов из N чисел, где каждое число — активация соответствующего перцептрона.
- Для исследования возьмём два перцептрона.
- Активации первого перцептрона для всех слов:
- Кролик — 0,9
- Слон — 0,87
- Кровать — 0,2
- Стол — 0,14
- Прыгнуть — -0,7
- Бежать — -1
Можно предположить, что выбранный перцептрон отвечает за распознавание животных, поскольку у слов «кролик» и «слон» активации выше, чем у существительных «кровать» и «стол», а у глаголов «бежать» и «прыгнуть» они и вовсе отрицательные.
- Активации второго перцептрона для всех слов:
- Кролик — 0,9
- Слон — 0,8
- Бежать — 0,6
- Прыгнуть — 0,55
- Стол — 0,1
- Кровать — 0
Наиболее высокие активации (0,9 и 0,8) наблюдаются для животных, средние активации (0,6 и 0,55) — для действий и низкие активации (0,1 и 0) — для предметов мебели. Исходя из этого, можно предположить, что данный нейрон отвечает за признаки, связанные с живыми существами и действиями. В этом случае перцептрон явно отвечает за несколько признаков, то есть полисемантичен. Объяснений его функций может быть масса.
Именно поэтому полисемантичные перцептроны мешают интерпретации нейросетей: они могут активироваться сразу на разных — зачастую совсем не схожих — входных данных, из-за чего сложно понять их назначения. Задача интерпретации была бы значительно проще, если каждый перцептрон активировался на один признак.
К решению именно этой проблемы приблизились исследователи компании Anthropic. Они разработали способ, который позволяет «разбить» полисемантичный перцептрон на набор моносемантичных. О том, как именно работает метод, мы расскажем во второй части материала.
Источник: Toy Models of Superposition: https://transformer-circuits.pub/2022/toy_model/index.html (дата обращения: 21.07.2024).


