Одно дерево решений хорошо, а сотни — ещё лучше
Random forest («случайный лес») — это алгоритм машинного обучения, который состоит из множества отдельных решающих деревьев, то есть из независимых моделей. У «Системного Блока» уже есть статья про решающие деревья, поэтому сначала рекомендуем ознакомиться с ней.
Важно, что в random forest каждое дерево строится независимо друг от друга на разных подвыборках обучающих данных. При этом при обучении каждого дерева используются разные комбинации признаков (характеристик) объектов, для которых делается предсказание, — поэтому деревья не похожи друг на друга.
Благодаря разнообразию деревьев можно повысить точность предсказания относительно точности отдельного дерева. При этом ансамбль помогает избежать переобучения, то есть ситуации, когда модель работает хорошо только на обучающей выборке. Такая проблема характерна для отдельных решающих деревьев.
Модель используется для задач классификации (предсказание класса, например, к какому семейству принадлежит растение) и регрессии (предсказание непрерывной величины — на сколько градусов повысится средняя температура зимой).
Как работает алгоритм?
Для того, чтобы обучить случайный лес и получить предсказания, используется метод беггинга (от англ. bootstrap aggregation). Рассмотрим этот процесс пошагово.
1. Подготовка обучающей выборки для одного дерева
Для обучения каждого дерева решений в random forest создаётся специальный набор данных — подвыборка. Она имеет характеристики, которые разработчик задаёт самостоятельно. Во-первых, можно менять размер: в неё может войти, например, половина или треть примеров из всей обучающей выборки, при этом некоторые примеры могут повторяться. Создание подвыборки таким способом называется бутстрап-семплированием (bootstrap-sampling).
Во-вторых, можно использовать разный набор признаков, которые будут содержаться в подвыборке. В ансамбле для построения моделей каждый раз используется случайный набор признаков. Например, если мы хотим предсказать вид растения, одна модель будет опираться на размер плодов и их цвет, а другая — на высоту стебля и форму листьев.
Рассмотрим более подробный пример. Представим, что мы решаем задачу классификации сорта яблока. У нас есть следующие данные, которые мы планируем использовать для обучения модели (для простоты объяснения мы используем маленькую выборку):
| Цвет плода | Вес плода (в граммах) | Количество семян | Вкус | Сорт (целевая переменная) |
| жёлтый | 220 | 3 | кисло-сладкий | Голден |
| зелёный | 200 | 4 | кисло-сладкий | Голден |
| зелёный | 210 | 5 | кислый | Голден |
| жёлтый | 150 | 4 | кисло-сладкий | Антоновка |
| зелёный | 120 | 5 | сладкий | Антоновка |
Случайно выберем из общего набора четыре последних наблюдения и сформируем подвыборку:
| Цвет плода | Вес плода (в граммах) | Количество семян | Вкус | Сорт (целевая переменная) |
| зелёный | 200 | 4 | кисло-сладкий | Голден |
| зелёный | 210 | 5 | кислый | Голден |
| жёлтый | 150 | 4 | кисло-сладкий | Антоновка |
| зелёный | 120 | 5 | сладкий | Антоновка |
В исходной выборке есть четыре признака (цвет и вес плода, количество семян, вкус), на которые алгоритм может опираться при предсказании. Чтобы построить дерево, выберем два случайных признака, например, цвет плода и его вкус:
| Цвет плода | Вкус | Сорт (целевая переменная) |
| зелёный | кисло-сладкий | Голден |
| зелёный | кислый | Голден |
| жёлтый | кисло-сладкий | Антоновка |
| зелёный | сладкий | Антоновка |
Этот набор данных понадобится для обучения одного дерева.
2. Обучение дерева
Построим дерево решений по собранной выборке:
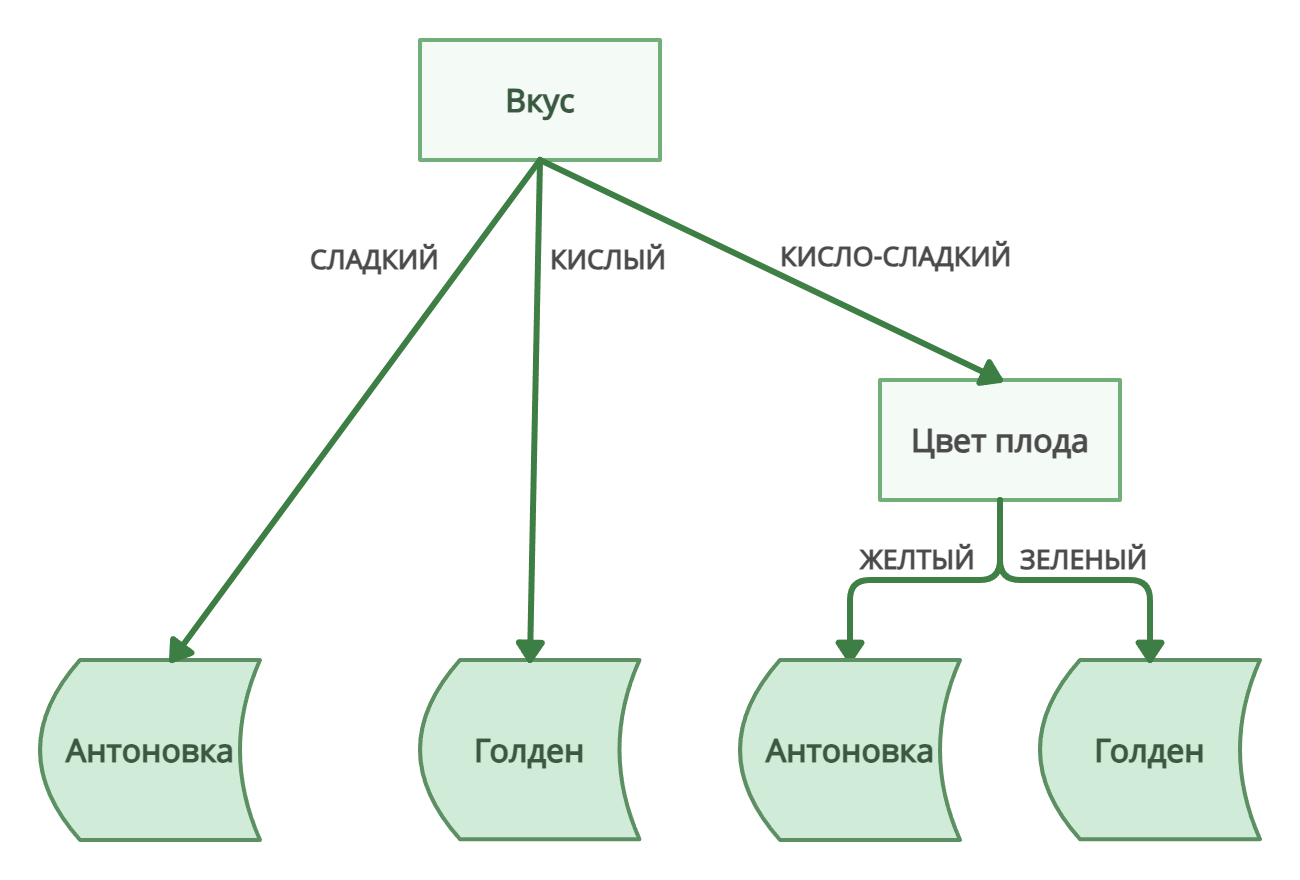
Дерево решений
Если бы мы остановились только на одном дереве решений, с высокой долей вероятности мы бы «обрезали» его: исключили слишком глубокие и подробные развилки, чтобы модель опиралась на общие закономерности в обучающих данных, а не просто запоминала все данные. Это позволило бы исключить переобучение. Однако в random forest деревья могут быть довольно глубокими, так как их количество и разнообразие компенсирует переобучение каждого конкретного дерева.
3. Делаем ансамбль — «высаживаем» много деревьев
Повторяем шаги 1 и 2: строим много деревьев на разных подвыборках с разными случайными признаками. Количество деревьев может варьироваться, оптимальное число обычно находится опытным путём.
4. Предсказываем!
В random forest демократия: деревья принимают решение путём голосования. Сначала каждое дерево даёт своё предсказание, а затем вычисляется итоговое предсказание леса: для задачи классификации по принципу большинства, для регрессии — усреднением всех значений.
Например, если за «Голден» проголосовали 60 деревьев, а за «Антоновку» — 40, алгоритм остановится на «Голден». Если бы мы предсказывали не класс, а, скажем, количество семян в яблоке (то есть решали задачу регрессии), алгоритм бы посчитал среднее арифметическое. К примеру, ответы деревьев такие: 150, 200, 170, 170, 210. Лес выдаст: (150+200+170+170+210) / 5 = 180.
Как оценить точность модели?
Чтобы проверить, насколько хорошо random forest справляется с задачей, можно посчитать метрику out-of-bag error (не единственный, но распространённый вариант). Процедуру можно описать так:
Шаги 2–4 описывают, что происходит с одним примером из выборки, но затем всё то же самое повторяется со остальными примерами.
- Формируется тестовая выборка. Напоминаем, что для обучения каждого дерева использовались не все данные. Для каждого дерева определяем, какие примеры не использовались для обучения, и добавляем их в тестовую выборку.
- Отбираются деревья, которые не обучались ни на одном примере из тестовой выборки.
- Для этого примера отобранные деревья делают свои предсказания. Затем выбирается общий итоговый ответ с помощью голосования (для классификации — большинством, для регрессии — усреднением значений).
- Считается out-of-bag error для одного примера: сравниваем фактическое и предсказанное значения. В случае классификации, если фактическое и предсказанное значения совпадают, ошибка равна 0, иначе — 1. При регрессии рассчитывается квадратичное отклонение.
- После повторения шагов 2–4 мы имеем набор данных об ошибках для каждого примера из тестовой выборки.
- Финальное значение out-of-bag error считается как среднее всех ошибок. Итого в задачах классификации получаем долю неправильных предсказаний среди всех предсказаний, а в задачах регрессии — среднее квадратичное отклонение.
На качество модели могут влиять разные факторы: количество признаков в подвыборках, количество деревьев, максимально возможная глубина деревьев. Универсальных рекомендаций не существует: нужно перебирать разные комбинации и измерять качество моделей.
Какие у random forest есть преимущества и ограничения?
Переобучение ансамбля — по сравнению с одиночным деревом — менее вероятно. Чем «глубже» дерево, тем точнее оно описывает конкретную выборку, но тем хуже оно будет предсказывать результаты для новых данных. Глубину построения дерева можно регулировать, тем самым влиять на обобщаемость модели, но на практике довольно сложно найти баланс. Для отдельного дерева это серьёзная проблема, но если в принятии решения участвует много глубоких деревьев, переобучение отдельной модели некритично, поскольку благодаря случайному выбору данных и признаков для каждого дерева корреляция между деревьями невысокая: их решения не связаны между собой, они независимы.
Алгоритм решающего дерева — один из самых легко интерпретируемых (исследователь может восстановить логику принятия решения, выявить значимые значения признаков, повлиявших на решение), однако проанализировать ансамбль деревьев куда сложнее. Для некоторых задач принципиально важно не только получить точный результат, но и уметь объяснить его (например, в медицине). В таких случаях random forest использовать будет затруднительно.


