Косинусная близость — это другое название для косинуса угла между двумя векторами. Сначала разберёмся с вектором, затем с косинусом, а потом научимся его считать.
Что такое вектор
Компьютер может воспринимать объекты только в виде чисел. Поэтому прежде чем сравнивать товары, тексты или фильмы, их надо перевестия в векторы — упорядоченные наборы чисел. Мы уже писали, как именно слова и изображения представляются векторами. Главная идея заключается в сопоставлении объекту нескольких чисел, каждое из которых характеризует какой-то признак объекта, например цвет и размер товара, тональность текста, жанр и длительность фильма.
Вектор можно визуализировать. Рассмотрим пример с представлением рюкзака через две характеристики — объём и количество отделений:
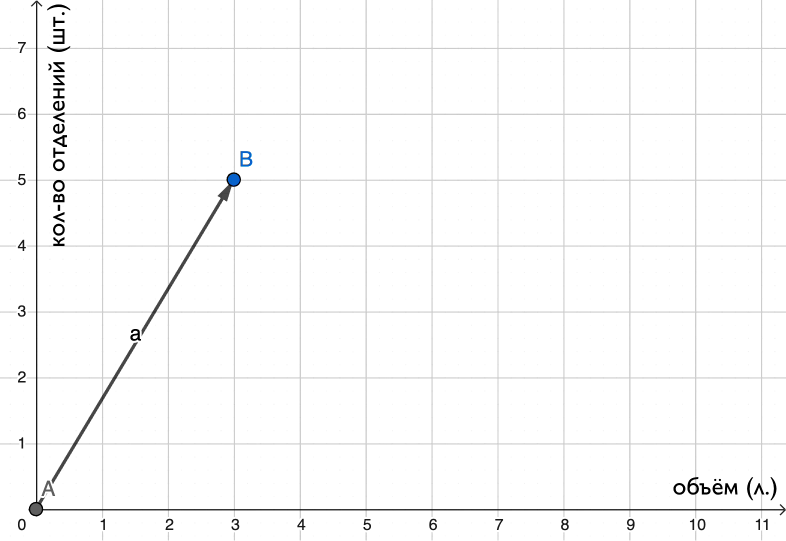
На координатной плоскости вектор соответствует рюкзаку с объёмом 3 литра (координата по горизонтальной оси) и пятью отделениями (координата по вертикальной оси). Чем больше признаков у объекта, тем больше чисел в векторе (эти числа называют координатами вектора). Например, рюкзак также может иметь признак «цена» — тогда соответствующий ему вектор будет располагаться не на плоскости, а в трёхмерном пространстве.
Вектор имеет две характеристики: направление и длину. Длина вектора вычисляется по следующей формуле:
Рассчитаем длину для вектора из примера с рюкзаком:
Между двумя векторами можно измерять расстояние и угол. Расстояние между векторами зависит от их длин, а угол между векторами нет: вы можете удлинять или укорачивать векторы («стрелки»), но угол между ними меняться не будет. Это важное свойство косинуса, поскольку во многих задачах длины векторов не важны.
Чем «ближе» векторы друг к другу (другими словами, чем меньше между ними расстояние или чем меньше угол между ними), тем более схожи соответствующие объекты. С помощью этого свойства компьютер может сравнивать объекты. На этом основан алгоритм KNN.
Как найти угол между векторами и причём здесь косинус
Угол между векторами и угол между прямыми по смыслу не отличаются. В случае векторов есть простая формула, которая позволяет рассчитать угол между ними по их координатам. Измерять угол в градусах (или радианах) не всегда бывает удобно. Гораздо удобнее выражать угол через его косинус.
Косинус — это одна из тригонометрических функций, которая на вход принимает угол и сопоставляет ему число из диапазона от -1 до 1. У косинуса есть геометрический смысл, однако для практических приложений он не так важен. Чем меньше угол, тем больше его косинус (это выполняется для углов в диапазоне от 0 до 180 градусов). Несколько важных значений косинуса:
- косинус 0 градусов равен 1 — направления векторов совпадают,
- косинус 60 градусов равен 0.5,
- косинус 90 градусов равен 0 — векторы перпендикулярны,
- косинус 180 градусов равен -1 — направления векторов противоположны.
Чем меньше угол между векторами, тем более схожи соответствующие объекты, и наоборот. Поэтому косинус между векторами также называют косинусной близостью.
Например, объекты, у которых соответствующие им векторы направлены одинаково (угол между ними 0 градусов), имеют с точки зрения косинуса максимальную близость, равную единице, а объекты, векторы которых указывают в противоположные направления (угол между ними 180 градусов), максимально удалены — у них косинус равен -1.
Чтобы найти косинус угла между векторами, надо:
1) рассчитать скалярное произведение векторов. Скалярное произведение двух векторов — это сумма произведений соответствующих координат векторов:
где ![]() и
и ![]() — это векторы, которые надо сравнить,
— это векторы, которые надо сравнить,
2) рассчитать произведение их длин,
3) разделить первое на второе:
Из формулы видно, почему косинус между векторами не зависит от длины вектора: увеличить длину вектор в N раз равносильно умножению всех его координат на N, поэтому при таком увеличении N в числителе сократится с N в знаменателе.
Разберём формулу на примере: найдём косинусную близость между следующими рюкзаками:
- рюкзак
с признаками «объём = 3 литра» и «кол-во отделений = 5 штук»,
- рюкзак
с признаками «объём = 5 литра» и «кол-во отделений = 2 штук».
Чтобы найти скалярное произведение по координатам векторов, надо попарно перемножить соответствующие координаты, а затем сложить произведения:
Теперь рассчитаем произведение длин векторов:

Остаётся только разделить разделить первое значение на второе:
Этот косинус соответствует углу 37 градусов.
Как посчитать косинусную близость с помощью компьютера
В Python найти косинусную близость между векторами можно с помощью библиотеки numpy, которая позволяет делать математические расчёты.
1. Загрузим библиотеку.
import numpy as np2. Напишем функцию get_cos_sim, которая будет рассчитывать косинус угла между векторами.
def get_cos_sim(a, b):
return a.dot(b) / (np.linalg.norm(a) * np.linalg.norm(b))Функция dot() рассчитывает скалярное произведение, а np.linalg.norm()— длину вектора.
3. Зададим векторы рюкзаков.
backpack_1 = np.array([2, 6])
backpack_2 = np.array([1, 2])
backpack_3 = np.array([4, 2])4. Рассчитаем косинусную близость между векторами.
cos_sim_1_2 = get_cos_sim(backpack_1, backpack_2)
cos_sim_1_3 = get_cos_sim(backpack_1, backpack_3)
print(cos_sim_1_2)
print(cos_sim_1_3)
>>0.9899494936611664
>>0.7071067811865475Получается, с точки зрения косинуса первый рюкзак более схож со вторым, нежели чем с третьим.
Мы также сделали проект в Google Colab, где вы можете попробовать рассчитать косинусную близость между разными словами. Для этого слова переводятся в векторы с помощью модели Word2Vec. Попробуйте сравнить слова «кошка», «собака» и «волк». Что ближе к «волку» — «кошка» или «собака»?


